A jegyzetről
Ez egy személyes jegyzet, amely csak a könnyű hozzáférés érdekében érhető el publikusan. Mivel a jegyzet saját felhasználásra készül, sok helyen hiányos, hibás. Helyenként üres oldalakat tartalmaz.
Ha mégis ráleltél és hasznosnak találod, én örülök, de ne kizárólag ezt a forrást használd felkészüléshez, ne is idézd sehol!
A tartalom helyességéért, teljességéért tehát felelősséget nem vállalok!
Órarend
| ⏰ | Hétfő | Kedd | Szerda |
|---|---|---|---|
| 8:00 |
Számítógépes grafika Gy (1)
Déli Tömb 2-219 |
Szoftvertechnológia Ea (F)
Aszinkron online |
Analízis II. Ea (F)
Déli Tömb 0-803 Szabó József eloadó / Számítógépes grafika Ea |
| 9:00 | |||
| 10:00 |
Analízis II. Gy (F) (1)
Északi Tömb -1.62 |
A számításelmélet alapjai I. Ea
Déli Tömb 0-822 Mogyoródi József terem |
A számításelmélet alapjai I. Gy (2)
Déli Tömb 00-115 |
| 11:00 | |||
| 12:00 |
Szoftvertechnológia Gy (F) (8)
Déli Tömb 00-411 (PC 7) |
Adatbázisok I. Ea (2)
Déli Tömb 0-821 Bolyai János terem |
|
| 13:00 | |||
| 14:00 | — | — | |
| 15:00 |
Operációs rendszerek Gy (12)
Déli Tömb 2-108 |
||
| 16:00 |
Adatbázisok I. Gy (10)
Északi Tömb 7.15 (PC 11) |
||
| 17:00 |
Operációs rendszerek Ea (91)
Déli Tömb 0-822 Mogyoródi József terem |
||
| 18:00 |
Szoftver mély neuronhálók alkalmazásához Gy
Északi Tömb -1.75 Konferenciaterem |
||
| 19:00 |
A számításelmélet alapjai I. előadás
Alapadatok
Idő: Kedd, 10:00 - 12:00
Helyszín: Déli Tömb 0-822 Mogyoródi József terem
Oktató: Tichler Krisztián, ktichler@inf.elte.hu
Csoport: 1
Értékelés
- Írásbeli vizsga
- max 60p (20p igaz-hamis, 20p rövid válasz, 20p hosszabb válasz)
- min ?
- Elővizsga: nem kötelező
Források
Alapfogalmak, nyelvek, grammatikák
- Alapfogalmak, nyelvek, grammatikák
Hol használják a formális nyelveket?
- A természetes nyelvek gépi feldolgozása, matematikai modellezése.
- Programozási nyelvek, fordítóprogramok
- Kódelmélet
- Mintafelismerés
Alapfogalmak, jelölések
- Ábécé:* egy véges, nemürres halmaz.
- Betűk: az ábécé elemei.
- Szó, (string): Egy ábécé elemeiből képzett véges sorozat.
- Egy szóban lévő betűk számát a szó hosszának nevezzük. ( = n)
- : üres szó
- jelöli a ábécé feletti szavak halmazát, beleértve az üres szót is.
- \
A szavait hosszlexikografikus (shortlex) rendezés szerinti sorrendben soroljuk fel.
- Résszó: az szó a szó résszava, ha
- Valódi résszó: ha és
- Prefix: ha
- Suffix ha
Ezek valódiak, ha -tól és -tól küéönböznek.
-
Nyelv: egy egy részhalmaza.
-
Üres nyelv:
-
Véges nyelv: véges, ellenkező esetben végtelen nyelv
-
Prefix nyelv:
-
Suffox nyelv:
Példák:
- (véges)
- (végtelen)
- (végtelen)
Műveletek szavakon
Konkatenáció
Legyen V egy ábécé továbbá legyenek és V feletti szavak. Ekkor az szót az és a konkatenáltjának nevezzük.
A konkatenáció mint művelet asszciatív, de általában nem kommutatív.
a konkatenáció műveletére zárt.
A konkatenáció egységelemes művelet, at egységelem az .
-edik hatvány: egy szó -szeres konkatanációja saját magával. ()
Formálisan:
Ekkor:
Tükörkép
Legyen egy ábécé feletti szó. Az szó -rel jelölt tükörképe (vagy megfordítottja) az a szó, amelyet úgy kapunk, hogy betűit az eredetihez képest fordított sorrendben konkatenáljuk. Vagyis i-edik betűje éppen -nak az . betűje .
Ha , akkor -t palindrom-nak nevezük.
Műveletek nyelveken
- Halmazműveletek ()
- Komplementer jelölése:
- Konkatenáció:
- asszociatív
- nem kommutatív
- -edik hatvány
- Tükörkép:
Egy nyelv iteratív leárt
Az nyelv iteratív lezártja (kleene-lezártja):
AZ pozitív lezártja:
, ha és , ha .
Homomorfizmus
Legyen és két ábécé. A leképezést homomorfizmusnak nevezzük, ha teljesülnek a következő feltételek:
- egyértelmű, azaz minden szóra pontosan egy szó létezik, amelyre teljesül.
- , minden -ra.
h-homomorf képi
Legyen homomorfizmus. A homomorfizmus -mentes, ha bármely szóra. Legyen homomorfizmus. Az nyelv h-homomorf képén a nyelvet értjük.
Formális nyelvek megadása
- Véges nyelvek esetén felsorolással
- Formulával
- Reguláris kifelyezéssel
- Végtelen nyelvek esetén felsoroló algortimussal
- Generatív grammatikákkal
- A grammatikák szintetizáló eszközök, egyetlen szimbólumból egy szabályrendszer segítségével szavakat lehet felépíteni. Azon szavak halmaza, melyeket fel lehet építeni egy nyelvet határoz meg, tehát a grammatika szabályrendszere meghatároz egy nyelvet.
- Matematikai gépek, automaták segítségével
- Az automaták elemző, analitikus eszközök. Az automaták bemenete egy szó, kimenete egy bináris érték. Az automata szabályrendszere szerint feldolgozza a szavakat, csak bizonyos szavak esetén ad igen választ, ezen szavak egy nyelvet alkotnak, melyet az automata szabályrendszere határoz meg.
Figyelem! Nem feltétlen lehet minden eszközzel minden nyelvet megadni. Be fogjuk látni például, hogy reguláris kifejezéssel kevesebb nyelvet lehet leírni mint egy általános grammatikával, de az se elég az összes {0, 1} ábécé feletti nyelv leírásához.
Nyelvcsalások
Ha egy halmaz, jelölje az halmaz hatványhalmazát, azaz
Nyelvcsalád alatt nyelveknek egy halmazát értjük.
Grammatikák
Egy rendezett négyest grammatikának nevezünk, ha
- és diszjunkt véges ábácék. elemeit nemterminális, elemeit pedig terminális szimbólumnak nevezzük.
- a grammatika kezdőszimbóluma
- rendezett párok véges halmaza, ahol és legalább egy nemterminális szimbólumot tartalmaz
A halmaz elemeit szabályoknak (vagy átírási szabályoknak vagy produkcióknak) hívjuk.
A gyakorlatban az jelölés helyett szinte mindig az jelölést használjuk.
Egylépéses levezetés
Legyen egy generatív grammatika és legyen .
A szó közvetlenül vagy egy lépésben levezethető az szóból -ben,
jelölése: , ha és
, ahol és .
Többlépéses levezetés
Legyen egy generatív grammatika és legyen .
A szó (több lépésben) levezethető, ha vagy van olyan és , hogy
és
Jelölés:
Reláció reflexív, tranzitív lezártja


Generált nyelv
Legyen egy tetszőleges generatív grammatika. A grammatika által generált nyelv alatt az szavakból álló halmazt értjük.
Vegyük észre, hogy a generált nyelv szavai mindig terminális szavak!
Források
Grammatikák csoportosítása
Grammatikák - ismétlés
Egy rendezett négyest grammatikának nevezünk, ha
- és diszjunkt véges ábácék. elemeit nemterminális, elemeit pedig terminális szimbólumnak nevezzük.
- a grammatika kezdőszimbóluma
- rendezett párok véges halmaza, ahol és legalább egy nemterminális szimbólumot tartalmaz
A halmaz elemeit szabályoknak (vagy átírási szabályoknak vagy produkcióknak) hívjuk.
A gyakorlatban az jelölés helyett szinte mindig az jelölést használjuk.
Legyen egy generatív grammatika és legyen .
A szó közvetlenül vagy egy lépésben levezethető az szóból -ben,
jelölése: , ha és
, ahol és .
Legyen egy generatív grammatika és legyen .
A szó (több lépésben) levezethető, ha vagy van olyan és , hogy
és
Jelölés:
Grammatikák Chomsky féle osztályozása
Legyen egy grammatika. A grammatika -típusú (), ha szabályhalmazára teljesülnek a következők:
- eset: nincs korlátozás
- eset:
- minden szabálya alakú, ahol és
- Egyetlen kivételt megengedünk: tartalmazhatja az szabályt, de csak abban az esetben, ha nem fordul elő egyetlen szabályának jobb oldalán sem. Korlátozott szabály (KES)
- eset: minden szabálya alakú, ahol és
- eset: minden szabálya vagy vagy alakú, ahol és
Jelölje az -típusú gramatikák osztályát.
Grammatikák osztályba sorolása
Legyen egy grammatika. A következő esetek lehetségesek:
Lokálisan minden szabály -as és teljesül a KES.
Lokálisan minden szabály -as den nem teljesül a KES.
Lokálisan minden szabály -as, van -as szabály és teljesül a KES.
Lokálisan minden szabály -es, van nem -as szabály de nem teljesül a KES.
Lokálisan minden szabály -es, van nem -es szanály és teljesül a KES.
Van nem -es szabálya vagy minden szabály -es, van nem
-es szabálya és nem teljesül a KES.
jelöli az -típusú nyelvek nyelvosztályát, elemeit -típusú nyelveknek nevezzük.
- A 0-típusú grammatikákat mondatszerkezetű (phrase-structure) grammatikáknak is nevezzük, ami nyelvészeti eredetükre utal.
- A 1-típusú grammatikák a környezetfüggő (context-sensitive) grammatikák, mert szabályai olyanok, hogy, egy A nemterminális valamely előfordulása egy szóval csak és kontextus jelenlétében helyettesíthető.
- 2-típusú grammatikákat környezetfüggetlen (context-free) grammatikáknak mondjuk, mert szabályai olyanok, hogy az nemterminális -vel való helyettesítése bármely kontextusban megengedett.
- A 3-típusú grammatikákat reguláris (regular) vagy véges állapotú (finite state) grammatikáknak hívjuk, a véges állapotú automatákkal való kapcsolatuk miatt.
- 0,1,2,3-típusú nyelvek osztályait rendre rekurzíven felsorolható, környezetfüggő, környezetfüggetlen, valamint reguláris nyelvosztálynak is mondjuk.
Grammatikák a gyakorlatban
- BNF (Backus-Naur Form).
A BNF egy széles körben használt metanyelv melynek segítségével szabályok alkothatók meg (például egy programozási nyelv szintaktikai szabályai).
Építőkövei:
- , fogalmak (nemdeterminánsok)
- a szabályok bal- és jobboldalának elválasztása
- a sztringek alkotóelemei (terminálisok)
Egy szabály bal- és jobboldalból áll, köztük ::=, baloldalon pontosan 1 fogalom, jobboldalon terminálisok és fogalmak véges sorozata állhat.
A BNF megfelel a környezetfüggetlen grammatikának.
Chomsky-féle hierarchia
A grammatikák alakja alapján és
Később azt is meg fogjuk mutatni, hogy a következö tétel fennáll:
Ekvivalens grammatikák és nyelvek
Amíg minden grammatika egyetlen nyelvet generál, ez fordítva nem igaz. Ugyanazt a nyelvet több különböz ̋o grammatika is generálhatja.
A és grammatikák ekvivalensek egymással, ha ugyanazt a nyelvet generálják, azaz teljesül.
Az és nyelveket egymással gyengén ekvivalensnek nevezzük, ha legfeljebb az tartalmazásában térnek el egymástól, azaz ha .
A és grammatikákat gyengén ekvivalensnek nevezzük, ha egymással gyengén ekvivalens nyelveket generálnak.
Terminánsok elimminációja a szabályok baloldalán
Minden grammatikához van vele ekvivalens és azonos típusú grammatika, melyre minden -re
Zártsági tulajdonságok
Az unió, konkatenáció és iteratív lezárás műveleteket reguláris műveleteknek nevezzük.
Egy nyelvcsalád zárt a -változós nyelvműveletekre nézve, ha minden esetén
zárt a reguláris műveletekre nézve ()
Források
Lineáris grammatikák, 3-típusú grammatikák normálformája, reguláriws kifelyezések
Lineáris grammatikák és nyelvek
Egy környezetfüggetlen grammatikát lineárisnak nevezünk, ha minden szabálya vagy
- vagy
- alakú, ahol és
A lineáris grammatikát bal-lineárisnak nevezzük, ha minden 2. alakú szabályban .
A lineáris grammatikát jobb-lineárisnak nevezünk, ha minden 2. alakú szabályban .
Bal és jobblineáris nyelvek
Egy nyelvet lineárisnak, bal-lineárisnak, illyetve jobb-lineárisnak mondunk, ha van olyan lineáris, bal-lineáris, illetve jobb-lineáris grammatika, amelyre teljesül.
Minden bal-lineáris grammatika reguláris (3-típusú) nyelvet generál.
L3 tükrözésre való zártsága
Minden jobb-lineáris grammatikához meg tudunk konstruálni egy bal-lineáris grammatikát, amely tükörképét generálja.
Következmény:
- zárt a tükrözés műveletére nézve.
- Minden reguláris nyelv generálható bal-lineáris grammatikával.
3-típusú grammatikák normálformája
Egy grammatika 3-as normálformájú, ha minden -beli szabály alakja
- vagy
- , ahol
Minden reguláris (azaz 3-típusú) nyelv generálható 3-as normálformájú grammatikával.
Reguláris kifelyezések
Vegyük észre, hogy minden véges nyelv reguláris. Tudjuk továbbá, hogy az nyelvosztály zárt az unió, a konkatenáció és az iteratív lezárt műveletekre nézve.
Következésképpen, kiindulva véges számú véges nyelvből és az előzőekben felsorolt reguláris műveleteket véges sokszor alkalmazva reguláris nyelvet kapunk.
Kérdés az, hogy vajon az eljárással minden reguláris nyelvet ekő tudunk-e állítani, azaz ez a módszer elégséges-e az nyelvosztály leírására?
Legyenek és diszjunkt ábécék. A ábécé feletti reguláris kifelyezéseket rekurzív módon következőképpen definiáljuk:
- reguláris kifejezés felett
- reguláris kifejezés felett
- reguláris kifejezés felett, ha
- Ha reguláris kifejezés felett, akkor is reguláris kifejezés felett
- Ha és reguláris kifejezések felett, akkor is
- Ha és reguláris kifejezések felett, akkor is
Minden egyes reguláris kifejezés egy-egy -rel jelölt reguláris nyelvet határoz meg, amelyeket az alábbi rekurzióval definiálunk:
- , ha reguláris kifejezés
- , ha reguláris kifejezések
- , ha reguláris kifejezések
A műveletek precedens sorrendje: , ennek és az asszociatív szabályok figyelembevételével bizonyos zárójelpárok elhagyhatók.
Leíró erő
Minden reguláris kifejezés reguláris nyelvet ír le, és megfordítva, minden reguláris nyelvhez megadható egy, ezen nyelvet leíró reguláris kifejezés.
Arden tétele
Ezt a tételt később a reguláris kifejezések véges automatákkal való kapcsolatának vizsgálatakor fogjuk használni.
Adottak az és reguláris kifejezések. A egyenletnek -re vonatkozó megoldása . Amennyiben , akkor az egyenletnek ez az egyetlen megoldása.
Források
Véges automaták
Formális nyelvek megadása nemcsak generatív eszközökkel, hanem felismerő eszközökkel is lehetséges. Ilyen eszközök az automaták, amelyek szavak feldolgozására és azonosítására alkalmasak.
Nyelvek megadására a grammatikák a szintetizáló, az automaták analitikus megközelítést alkalmaznak.
Az automaták egy szó feldolgozása után kétféle választ adhat, vagy elfogadja, vagy elutasítja a bemenetet.
- Diszkrét időintervallumokban végrehajtott lépések sorozatán keresztül működik
- A kezdőállípotból indul, az inputszó az inputszalagon helyezkedik el, az olvasófej őedig az inputszó legbaloldalibb szimbólumánál áll.
- Az automata, miután elolvasott egy szimbólumot, az olvasófejet egy pozícióval jobbra mozgatja, majd állapotot vált az állapot-átmenet függvénye szerint.
- Amennyiben az automata még nem olvasta végig a teljes inputot és elfogadó állapotba ér nem dönt még az elfogadásról/elutasításról, tovább m ̋uködik a szabályai szerint.
- Ha az automata elolvasta az inputot, akkor megáll és aktuális állapota alapján válaszol, hogy felismeri vagy elutasítja a bemeneti szót.
Determinisztikus véges automata
Egy rendezett ötös, ahol
- az állapotok véges, nemüres halmaza
- az inputszimbólumok ábécéje
- leképzés az ún. állapot-átmenet függvény
- a kezdőállapot
- az elfogadó állapotok halmaza
Az átmenetfüggvény kiterjesztése
Legyen egy determinisztikus véges automata.
A leképzés kiterjesztése az a teljes leképzés, amelyre
tehát az az állapota az automatának, ahova a állapotból indulva az szó feldolgozása után eljut.
Ha , akkor az inputot elfogadja , ha , akkor elutasítja.
elhagyjuk.
Nemdeterminisztikus véges automata
Determinisztikus véges automata:
- A függvény mindenütt értelmezett és egyértékű. Azaz minden párra pontosan egy olyan s állapot létezik, amelyre fennáll.
Nemdeterminisztikus véges automata:
- Megengedjük az állapot-átmenet függvény többértékűségét, azaz ekkor egy leképezés.
- Több kezdoállapot is megengedett (azaz a kezdőállapotok halmazára ).
- Úgy interpretálhatjuk, hogy a állapotból az betű olvasására a gép egy tetszoleges -beli új állapotba léphet, azaz adott inputra több működés lehetséges.
- Mivel , ezért elofordulhat, hogy az valamely -ra, ilyenkor elakad a gép.
- Akkor fogad el egy bemenetet, ha van legalább egy -beli állapotban termináló működése.
A nemdeterminisztikus véges automata egy rendezett ötös, ahol
- az állapotok egy véges, nemüres halmaza
- az inputszimbólumok ábécéje
- leképzés, az állapot-átmenet függvény
- a kezdőállapotok halmaza
- az elfogadó állapotok halmaza.
A determinisztikus véges automata a nemdeterminisztikus véges automata egy speciális esetének tekinthető.
Szabály alapú alternatív megközelítés
Legyen egy nemdeterminisztikus véges automata-
Az átmenetek szabály alapon történő megadása:
Az -hoz tartozó szabályrendszerhez minden esetén adjunk hozzá a alakú átírási szabályt, azaz
Redukció
Egylépéses redukció
Láttuk, hogy az automata további műuködése mindig csak az aktuális, állapottól és a bemenet még hátralévo olvasatlan suffixétol függ. Ez motiválja a következőt.
Egy szót az NDVA egy konfigurációjának nevezzük.
Legyen egy véges automata és legyenek konfigurációk. Az automata az szót egy lépésben a szóra redukálja, ha van olyan szabály, és olyan szó, hogy és teljesül.
Többlépéses Redukció
Az véges automata az szót a szóra redukálja, ha vagy vagy valamelyik -rw léteznek konfigurációk, melyekre és
Elfogadott elv
Az nemdeterminisztikus véges automata által elfogadott nyelv alatt az nyelvet értjük.
Véges automaták és reguláris nyelvek
Minden nemdeterminisztikus véges automatához meg tudunk adni egy 3-tíípusú grammatikát, úgí hogy teljesül.
Minden 3-típusú grammatikához meg tudunk adni egy nemdeterminisztikus véges automatát úgy, hogy teljesül.
Véges automata determinizálása
Minden nemdeterminisztikus véges automatákhoz megkonstruálható egy determinisztikus véges automata úgy, hogy teljesül.
Tehát mind a determinisztikus véges automaták, mind a nemdeterminisztikus véges automaták reguláris (-beli) nyelveket leíró formális eszközök.
Források
Véges automata determinizálása, összefüggő automaták, algoritmikus eldöntési probléma
- 5. Véges automata determinizálása, összefüggő automaták, algoritmikus eldöntési probléma
- Véges automata determinizálása
- L3 további zártsági tulajdonságia
- Összefüggő automata
- Algoritmikus problémák
- 3as típusú grammatikák algoritmikus problémái
- Eldönthető, hogy egy reguláris grammatika az üres nyelvet generálja-e.
- Eldönthető, hogy két reguláris grammatika által generált nyelv diszjunkt-e.
- Eldönthető, hogy két reguláris grammatika ugyanazt a nyelvet generálja-e vagy sem.
- Eldönthető, hogy egy reguláris grammatika bővebb, vagy egyenlő nyelvet generál-e, mint egy másik.
- A 3-as típusú grammatikák szóproblémája hatékonyan eldönthető.
- 3as típusú grammatikák algoritmikus problémái
- Források
Véges automata determinizálása
Minden véges nemdeterminisztikus automatához megkonstruálható egy véges determinisztikus automata úgy, hogy teljesül.
L3 további zártsági tulajdonságia
zárt a komplementerre, a metszetre és a különbségre.
Tehát az alábbi formális eszközök mind az nyelvosztályt írják le egy adot ábécé felett:
- jobblineáris grammatikák
- ballineáris grammatikák
- 3-as normálformájú grammatikák
- reguláris kifelyezések
- a komplementer, metszet, különbség, tükörkép, pozitív lezárt műveletekkel bővített úgynevezett általánosított kifejezések
- véges determinisztikus automaták
- véges nemdeterminisztikus automaták
Összefüggő automata
Legyen véges determinisztikus automata. A állapotot a kezdőállapotból elérhetőnek mondjuk, ha létezik redukció, ahol
Az véges determinisztikus automatát összefüggőnek mondjuk, ha minden állapota elérhető a kezdőállapotból.
elérhető a kezdőállapotból, akkor és csak akkor, ha van olyan , hogy
Algoritmikus problémák
Akkor beszélünk algoritmukis eldöntési problémáról, ha a bemenet egy olyan objektum, mely egy adott végtelen halmazból kerülhet ki, kimenete pedig igen/nem.
Olyan algoritmust keresünk, amely kellően általános ahhoz, hogy a végtelen lehetséges bemenet bármelyike esetén alkalmazható legyen.
Egy probléma eldönthető, ha létezik olyan minden lehetséges bemenet esetén termináló algoritmus, amelyik a helyes választ adja.
3as típusú grammatikák algoritmikus problémái
Eldönthető, hogy egy reguláris grammatika az üres nyelvet generálja-e.
Bizonyítás: A tanultak szerint a grammatikához megadható olyan A véges determinisztikus automata, amelyik a grammatika által generált nyelvet ismeri fel. Az automata pontosan akkor nem ismer fel egyetlen szót sem, ha kezdőállapotából minden végállapota elérhetetlen. Ez viszont algoritmikusan eldönthető.
Eldönthető, hogy két reguláris grammatika által generált nyelv diszjunkt-e.
Bizonyítás: Generálják a és reguláris grammatikák rendre az és nyelveket. Az nyelv szintén reguláris, így van olyan reguláris grammatika, amely -at generálja. Ekkor azonban akkor és csak akkor, ha , amely a fentiek szerint eldönthető.
Eldönthető, hogy két reguláris grammatika ugyanazt a nyelvet generálja-e vagy sem.
Bizonyítás: Generálják a és reguláris grammatikák rendre az és nyelveket. Az nyelv szintén reguláris, így van olyan reguláris grammatika, amely -at generálja. Ekkor azonban akkor és csak akkor, ha , amely a fentiek szerint eldönthető.
Eldönthető, hogy egy reguláris grammatika bővebb, vagy egyenlő nyelvet generál-e, mint egy másik.
Bizonyítás: Generálják a és reguláris grammatikák rendre az és nyelveket. Az szintén reguláris. Ennek üressége eldönthető, ami ekvivalens azzal, hogy
A 3-as típusú grammatikák szóproblémája hatékonyan eldönthető.
Szóprobléma: Adott grammatika és .
Bizonyítás: Legyen egy 3-as típusú grammatika normálformában adva és a levezetendő szó.
Az algoritmus rekurzívan kiszámol egy részhalmazból álló sorozatot. -ból (csak -től függő) konstans időben számolható.
Könnyen látható, hogy azon nemterminálosok halmaza, melyek pontosan leezetési lépés után a mondatforma végén állhatnak.
Tehát ha , akkot nyilván
Források
Maradéknyelv, myhill-nerode tétel, minimális-, redukált-, faktor automata,
Maradéknyelv
Nyelv adott szóra vonatkozó maradéknyelve
Az és automaták ekvivalensek, ha .
Adott nyelv -ra szóra vonatkozó maradéknyelve , ahol
tehát azokat a szavakat tartalmazza, amelyekkel -t jobbról kiegészítve -beli szót kapunk.
Automata adott állapotra vonatkozó maradéknyelve
Legyen véges determinisztikus automata.
Az L(A, q) \coloneqq {v \in \Sigma^* \vert\ qv \implies p, p \in F} nyelvet az automata állapotra vonatkozó maradék nyelvének nevezzük.
Alternatív definíció:
Az tehát azokat a szavakat tartalmazza, amelyek hatására az automata -ból indítva végállapotba kerül.
Azaz, lenne az elfogadott nyelv, ha a kezd˝oállapotot q-ra változtatnánk.
Tulajdonságai:
Myhill Nerode tétel
ahol az nyelv ábécéje.
Példa
.
Ekkor
.
Tehát ez a végtelen sok maradéknyelv páronként különböző, így
ZH-n jól használható determinisztikus automata kreálására!
Minimális automata
Mivel állapothalmaza , ezért az alábbi következményt kapjuk:
Az automata állapotszáma kisebb vagy egyenlő, mint a tetszőleges, az nyelvhez adott véges, determinisztikus automata állapotszáma.
Az véges determinisztikus automata minimális állapotszámú, ha nincs olyan -val ekvivalens véges determinisztikus automata, aminek kevesebb állapota van mint -nak. Egy nyelv minimális automatája alatt egy -et felismerő minimális véges determinisztikus automatát értünk.
Minimális automata készítése
Cél: Adott automatához minél kevesebb állapotú, vele ekvivalens, azaz az eredeti automata által felismert nyelvet elfogadó automatát megadni. Két lépésben fogjuk ezt elérni:
- Összefüggővé alakítás:
Nyilván átmeneteikkel együtt elhagyhatók azok az állapotok, melyekbe nem tud eljutni az automata. Az átmenetdiagramon ez annak felel meg, hogy nincs a kezd˝oállapotból irányított út a csúcsba.
- Ekvivalens állapotok összevonása:
Ha két állapotból pontosan ugyanazon szavak hatására kerül az automata végállapotba, akkor az elfogadás szempontjából mindegy, hogy a m˝uködés során a két állapotba kezül melyikbe került az automata. Ezek az állapotok nyilván összevonhatók.
Redukált automata
Legyenek állapotok. -t és -t nevezzük megkülönbözhetetlennek, ha
Egy véges determinisztikus automata redukált, ha nincsenek megkülönböztethetetlen állapotai.
Faktorautomata
Legyenek és véges, determinisztikus automaták. A két automata izomorf, ha van olyan bijekció, melyre
- esetén
Tétel:
Az determinisztikus véges automata ~ faktorautomatája
- ekvivalens -val
- redukált
- ha összefüggő, akkor izomorfia erejéig az egyetlen összefüggő, redukált -val ekvivalens automata.
Összegzés
Tehát egy A véges determinisztikus automatához minimális automatát készíthetünk úgy, hogy
- az elérhetetlen állapotait elhagyjuk ezzel előállítva egy -val ekvivalens összefüggő automatát,
- majd a már összefüggő automata relációnak meghatározása segítségével a fenti módon algoritmikusan előállítunk egy redukált automatát.
- Az így kapott automata, összefüggő, redukált és ekvivalens -val, ezért korábbi tételünk alapján izomorf az -vel,
- mivel az automata, ahol szintén összefüggő, redukált (minden minimális automata redukált kell legyen) és -val ekvivalens, ezért ugyanezen tétel alapján szintén izomorf a faktorautomatával,
- mivel minimális automata, ezért a faktorautomata és az által algoritmikusan meghatározott automata is minimális automata, tételünk szerint ezek izomorfak egymással.
Források
Nyelvi egyenletrendszerek megoldása, általánosított automata
Lineáris nyelvi egyenletrendszerek megoldása
Arden tétele általánosabban:
Legyenek az és nyelvek adottak. Az X = L_1 X \cup \L_2 egyenletnek -re vonatkozó megoldása . Amennyiben , akkor az egyenletnek ez az egyetlen megoldása.
Legyen nyelvi egyenletrendszer, ahol az nyelvmátrix és a nyelvvektor adott az ismeretlen nyelvekből álló vektort keressük. Ha és , akkor az egyenletrendszernek egyértelműen létezik -beli megoldása, és ez a megoldás elemeiből a reguláris nyelvműveletekkel épül fel.
Automata adott állapotra vonatkozó maradéknyelve
Egy determinisztikus véges automata egy állapotra vinatkozó maradéknyelve alatt az nyelvet értjük.
Az tehát azokat a szavakat tartalmazza, amelyek hatására az automata -ból végállapotba kerül.
Tehát és
Vegyük továbbá észre, hogy fennállnak a következő nyelvi egyenletek:
ahol
A maradéknyelvekre vonatkozó egyenletrendszert megoldjuk ( az érdekes). A megoldás egyértelműsége az előző tételből, de az -k egyértelműségéből is adódik.
Általánosított automata
Legyen a feletti reguláris kifejezések halmaza.
Az általános automata definíciója megegyezik a véges nemdeterminisztikus automata definíciójával azzal a kivétellel, hogy átmenetfüggvényére teljesül.
Átmenetdiagramon ábrázolva az általánosítás az, hogy az élek címkéi betűk helyett tetszőleges feletti reguláris kifejezések lehetnek.
Legyen egy általánosított automata és legyenek konfigurációk. Az automata az szót egy lépésben (közvetlenül) a szóra redukálja (jelölés: ), ha van olyan , hogy és teljesül.
A többlépéses redukció és a felismert nyelv fogalma nem változik.
Az -átmenetes, nemdeterminisztikus véges automata olyan általánosított automata, ahol minden átmenet -beli.
Tehát átmenetfüggvénye az input betűnkénti feldolgozása mellett állapotváltásokat engedélyezhet (-átmenetek).
Kis Bar-Hillel lemma
Minden nyelvhez van olyan konstans, hogy minden szó esetén ha tekintjünk egy tetszőleges olyan felbontását, ahol , akkor van -nek olyan részszava , hogy , és minden esetén .
Kevésbé formálisan: minden szavának elég hosszú részszavában létezik elég rövid, nemüres, beiterálható részszava.
Források
Környezetfüggetlen grammatikák, Chomsky normálforma, CYK algoritmus
Egy környezetfüggetlen grammatika szabályai alakúak, ahol
Egy környezetfüggetlen grammatika egy nemterminálisát aktívnak mondjuk, ha van olyan terminális szó, amire teljesül. Egyébként -et inaktív nevezzük.
Egy környezetfüggetlen grammatika egy nemterminálisát elérhetőnek nevezzük, ha léteznek olyan szavak, amelyekre teljesül. Egyébként -t elérhetetlennek (nem elérhetőnek) mondjuk.
Egy környezetfüggetlen grammatika egy nemterminálisát hasznosnak nevezzük, ha aktív és elérhető. redukált, ha minden nemterminálisa hasznos.
Redukált grammatika
Minden környezetfüggetlen grammatikához létezik vele ekvivalens redukált környezetfüggetlen grammatika.
Lépések:
- inaktívak elhagyása
- elérhetetlenek elhagyása
Chomsky normálforma
Egy grammatika Chomsky normálformájú, ha minden -beli szabály alakja a következők valamelyike:
- továbbá , ha
Minden környezetfüggetlen grammatikához létezik vele ekvivalens Chomsky normálformájú grammatika
Lépések:
- álterminálisok bevezetése
- hosszredukció
- -mentesítés
- láncmentesítés
Környezetfüggetlen grammatikák szóproblémája
Legyen egy környezetfüggetlen grammatika és egy egy szó. Eldönthető, hogy
A naiv algoritmzs csak exponenciális felső becslést adhatunk a szóprobléma eldöntésének hatékonységéra.
Dinamikus programozás segítségével megalkotott algoritmus már polinomiális lesz.
A CYK algoritmus Chomsky normálformában adott grammatika esetében nagyságrendűű lépésben eldönti a szóproblémát.
Tetszőleges környezetfüggetlen grammatika esetén tehát a Chomsky normálformára hozással kombinálva a CYK algoritmus hatékonysága
Források
9. Veremautomaták
-
Input szalag
-
Verem
-
Véges vezérlő
-
A veremautomata a véges automata általánosítása potenciálisan végtelen veremmel és véges kontrollal.
-
A verem esetében az új adat mindig a már meglév˝o veremtartalom tetejéhez adódik, kivétele fordított sorrendben történik.
-
alapértelmezetten nemdeterminisztikus
A veremautomata egy rendezett hetes, ahol
-
a veremszimbólumok véges halmaza
-
az állapotok véges halmaza
-
az inputszimbólumok véges halmaza
-
az úgynevezett átmeneti függvény
-
a kezdeti veremszimbólum
-
a kezdeti állapot
-
az elfogadó állapotok vagy végállapotok halmaza
-
A verem tetején lévő szimbólum, az aktuális állapot és az inputszimbólum együttesen határozzák meg a következő átmenetet.
-
Minden lépésben mindenképpen kiveszünk egyetlen egy elemet a verem tetejéről és beteszünk helyette néhányat. (0, 1, 2, darabot)
-
Ha nem üres, akkor ún. -átmenet hajtható végre, ami lehetővé teszi, hogy a veremautomata anélkül változtassa meg az állapotát és/vagy a verem tartalmát, hogy az inputszalagról betűt olvasna be.
-
-mozgásra lehetőség van már az első inputszimbólum elolvasása előtt is illetve még az utolsó inputszimbólum elolvasása után is.
Veremautomata konfigurációi
A veremautomata konfigurációja alatt egy alakú szót értünk, ahol a verem aktuális tartalma és az aktuális állapot és az input még feldolgozatlan része.
Kezdőkonfigurácicó:
Egylépéses redukció
Az veremautomata az konfigurációt a konfigurációra redukálja egy lépésben, amelyet -val jelölünk, ha létezik olyan és , hogy és és teljesül.
Többlépéses redukció és a felismert nyelv
Az veremautomata az konfigurációt a konfigurációra redukálja, amelyet -val jelöljük, ha vagy , vagy létezik olyan szavakból álló véges sorozat, ahol és
Az veremautomata által elfogadó állapottal felismert nyelv:
Determinisztikus veremautomata
Az veremautomatát determinisztikusnak nevezünk, ha minden esetén
Tehát minden és esetén
- vagy pontosan egy elemt tartalmaz, minden inoutszimbólumra és
- vagy pontosan egy elemet tartalmaz és minden inputszimbólumra.
Üres veremmel felismert nyelv
Az veremautomata által üres veremmel felsimert nyelv:
Vegyük észre, hogy ha a verem üres, akkor az automata működése blokkolódik, mivel nincs átmenet definiálva üres verem esetére.
Így a verem az input teljes feldolgozása után, az utolsó átmenettel kell üressé váljon.
Szintén a blokkolás elkerülése végett definiáltuk úgy a kezdőkonfigurációt, hogy a veremábécé egy eleme () már eleve a veremben van.
Az elfogadó állapotok halmaza irreleváns szempontjából.
Végállapottal vs üres veremmel elfogadás
Bármely veremautomatához meg tudunk adni egy veremautomatát, úgy, hogy teljesül
Bármely veremautomatához meg tudunk adni egy veremautomatát, úgy, hogy teljesül
Veremautomaták és környezetfüggetlen grammatikák
Bármely környezetfüggetlen grammatikához magkonstruálható egy olyan veremautomata, amelyre teljesül.
Minden veremautomatához megadható egy környezetfüggetlen grammatika úgy, hogy teljesül
Források
10. Levezetési fa - nincs jegyzet
Környezetfüggő grammatikák
Egy grammatikát hossz-nemcsökkentőnek mondunk, ha minden szabályának alakjára az alábbiak valamelyike teljesül:
- , de ha van ilyen szabály, nem lehet szabály jobb oldalán
- , ahol és
Minden hossz-nemcsökkentő grammatika környezetfüggő nyelvet generál.
Következmény:
Kuroda normálforma
Egy grammatikát Kuroda normálformájúnak mondunk, ha minden szabályának alakjára az alábbiak valamelyike teljesül:
- , de ha van ilyen szabály, nem lehet més szabály jobb oldalán.
Minen környezetfüggő grammatikához van vele ekvivalens Kuroda normálformájú grammatika.
A környezetfüggő nyelvek szóproblémája
Eldönthető, egy hossz-nemcsökkentő grammatika és szó esetén .
Egy 0-típusú normálforma
Bármely 0-típusú grammatikához van vele ekvivalens grammatika, ahol minden szabályának alakjára az alábbiak valamelyike teljesül:
- , de ha van ilyen szabály, nem lehet más szabály jobb oldalán.
Források
12. Előadás - nincs jegyzet
A számításelmélet alapjai I. gyakorlat
Alapadatok
Idő: Szerda, 10:00 - 12:00
Helyszín: Déli Tömb 00-115
Oktató: Tichler Krisztián
Csoport: 2
Értékelés
- 2 ZH, egyet lehet javítani
Források
Nyelvek
- Előadás ismétlése
- Előadás példáihoz hasonló feladatok.
Források
Grammatikák
Grammatikák megadása, generált nyelv meghatározása.
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
Grammatikák II
Források
Grammatikák III, reguláris kifejezések
Források
Véges automaták
Források
Zárthelyi
ZH megoldás, grammatikák visszamenőleg, általános automaták
Források
9. Általános automaták, Chmosky normálforma, CYK algoritmus
Források
Veremautomaták
Források
11. Gyakorlat - nincs jegyzet
Adatbázisok I. előadás
Alapadatok
Idő: Kedd, 12:00 - 14:00
Helyszín: Déli Tömb 0-821 Bólyai János terem
Oktató: Szalai-Gindl János Márk, szalaigindl@inf.elte.hu
Csoport: 2
Értékelés
- Írásbeli vizsga
- Ehhez lehalább 2-es gyakorlatjegy szükséges
- Elméleti és gyakorlati feladatok
- Beugró Canvason jelenlétben, aztán hosszabb, esszé jellegű feladatok
Források
Bevezetés és relációs adatmodell
Mi az az adatbázis?
Hátköznapi értelemben: összefüggő adatok praktikusan rendezett gyűjteménye és ezeknek valamilyen rendszerben való tárolása, amely a való világot valamilyen szempontból modellezi.
Adathalmaz adatbázis.
Ma már az élet számos területén alapvető fontossággal bírnak.
Példa: egyetemi oktatás
Tegyük fel, hogy egy olyan adatbázist szeretnénk, amely az egyetemi oktatásról készít modellt.
A dolgok, amelyeket tárolnunk kell:
- Infók az oktatókról
- azonosítószám
- név
- beosztás
- Tárgyakról
- név
- oktató azonosító
- bevezetés éve
- Termek használatáról
- épület
- szobaszám
- időköz
- tárgynév
Egy tárgyat egy vagy több oktató oktathat, egy oktató egy vagy több tárgyat oktathat.
Egy időben egy teremben csak egy tárgyat oktathatnak.
Nyers fájlok
Tároljuk az adatokat CSV fájlokban.
Használjunk egy-egy fájlt az oktatóra, a tárgyakra és a teremhasználatra!
Az alkalmazásunknak majd szintaktikai elemzést kell végezni minden egyes alkalommal a fájlokon, amikor olvasni/frisséteni fogja a bejegyzéseket.
Adatintegritás
Hogyan tudjuk azt biztosítani, hogy egy előadó az összes albumánál ugyanabban a formában jelenjen meg?
- Pl. adatbázis, adatbázisok, AB,
Mi történik, ha valaki véletlenül felülírja a tárgy bevezetésének évét egy érvénytelen stringgel?
- Pl. 1993 helyett ezerkilencszázkilencvenhérom.
Hogyan, milyen formában tároljuk, ha több oktató oktat egy tárgyat?
Implementáció
Hogyan keresünk meg egy adott bejegyzést?
Mi van, ha egy új alkalmazást akarunk készíteni, amelyik ugyanazt az adatbázist használja?
Mi van, ha két thread egyidőben ugyanabba a fájlba próbál írni?
Tartósság
Mi van, a a gép elszáll, miközben éppen egy bejegyzést frissítünk?
Mi van, ha a magas rendelkezésre állás érdekében többszörözni/másolni akarjuk ugyanazt az adatbázist több gépen?
Adatbázis definiálása
Az adatbázisnak új meghatározást adunk: olyan adatok együttese, amelyet egy adatbázis-kezelő rendszer (DBMS: Database Management System) kezel.
Az általános DBMS megoldandó feladatai:
- új adatbázisok létrehozása, ezek logikai szerkezetének, sémájának definiálása, adatdefiníciós nyelv (DDL - Data Definition Language)
- adatok lekérdezése, módosítása (DML - Data Manipulation Language)
- nagyméretű adatok hosszú időn keresztül történő tárolása, adatok biztonsága, meghibásodásokkal, illetéktelen hozzáférőkkel szemben, hatékony adatbázis-hozzáférés
- egyszerre több felhasználó egyidejű hozzáférésének biztosítása
Adatmodell fogalma
Az adatmodell információ vagy adatok leírására szolgáló jelölés.
A leírás részei:
- az adatok struktúrája
- az adatokon végezhető műveletek
- az adatra vonatkozó megszorítások
Legfontosabb modellek: relációs és féligstruktúrált (XML)
Relációs adatmodell
A relációs adatmodellben az adatokat kétdimenziós táblákban (relációkban) tároljuk.
A reláció fejrészében találhatók az attribútomok
Minden attribútomhoz hozzátartozik egy értékkészlet
A reláció neve és a reláció-attribútomok halmaza együtt alkotják a relációsémát
A reláció attribútumainak sorrendje felcserélhető.
A séma egy adatmodellben általánosságban azt adja meg, hogy egy-egy adatelem milyen "formájú" adatokat tárol.
Egy-egy reláció soroknak egy halmaza
Halmaz: nem számít a sorrend, egy elem csak egyszer szerepelhet.
A reláció sorainak halmazát előfordulásnak nevezzük.

esetén az attribútomok értékkészlete adja az alaphalmazokat (), egy egy előfordulás pedig egy-egy matematikai relációnak "feleltethető meg".
Az attribútumok sorrendje láttuk, hogy nem rögzített a relációsémában. Egy-egy előfordulás ábrázolása esetén viszont rögzítésre kerül.
A lényeg, hogy a soroknál egy attribútum értékét az attribútum nevével azonosítjuk, és nem pedig azzal, hogy hányadik helyen szerepel a soron belül.
Az adatbázis tulajdonképpen relációk halmaza. A megfelelő relációsémák halmaza adja az adatbázissémát, a hozzá tartozó előfordulások pedig az adatbázis-előfordulást.
Egy sor elemeit mezőnek (komponens) nevezzük. Minden mező csak atomi értéket vehet fel. Léteznek bonyolultabb adatmodellek is, ahol egy mező értéke lehet halmaz, lista, tömb, referencia stb.
Megjegyzés: a gyakorlatban sokszor megengedik a sorok ismétlődését, hiszen az ismétlődések megszüntetése nagyon időigényes
Megszorítás
Az attribútumok egy halmaza egy kulcsot alkot egy relációra nézve, ha a reláció bármely előfordulásában nincs két olyan sor, amelyek a kulcs összes attribútumának értékein megegyeznének.
pl. TAJ-szám...
A kulcsot aláhúzás jelöl: Teázó(név, város, tulaj)
Algebra
Egy algebra általában műveleteket és atomi operandusokat tartalmaz.
A relációs algebra lehetővé teszi kifejezések megfogalmazását az atomi operandusokon és az algebrai kifejezéseken végzett műveletek alkalmazásával kapott relációkon.
Fontos tehát, hogy minden művelet végeredménye reláció, amelyen további műveletek adhatók meg.
A relációs algebra atomi operandusai a következők:
- a relációkhoz reprezentáló változók
- konstansok, amelyek véges relációt fejeznek ki
Relációs algebra
- Projekció: Adott relációt vetít le az alsó indexben szereplő attribútumokra.

- Szelekció: Kiválasztja az argumentumban szereplő
reláció azon sorait, amelyek eleget tesznek az alsó indexben
szereplő feltételnek.

- Unió, metszet, különbség

- Descartes-szorzat

- Átnevezés: relációk adott attribútumanak átnevezése.
- Théta-összekapcsolás: összekapcsolás valamilyen predikátummal
- Természetes összekapcsolás: összekapcsolás predikátum nélkül
Egy relációkon értelmezett operátor akkor monoton, ha bármelyik argumentumrelációhoz egy újabb sort hozzávéve az eredmény tartalmazza az összes olyan sort, amelyet addig tartalmazott és esetleg újabb sorokat is.
Források
Relációs algebra lekérdezések optimizációja és bevezetés az SQL-be
- Relációs algebra lekérdezések optimizációja és bevezetés az SQL-be
Relációs algebra lekérdezések optimizációja
Cél: a feladatot minél kevesebb adatmozgatással tudjunk megoldani a háttértár és a központi memória között.
- Minél kevesebb disk I/O művelet végrehajtása egy-egy lekérdezés végrehajtása során.
- Az optimalizáció során relációs algebrai azonosságok alkalmazása. ()
- Eredetivel ekvivalens lekérdezés készítése, kiszámításához az esetek többségében kevesebb I/O művelet

Algebrai azonosságok
Descartes-szorzat és összekapcsolások

Projekció és szelekció

Kiválasztás és Descartes-szorzat/összekapcsolás


Projekció/kiválasztás és halmazműveletek

Optimizációs stratégiák
- Feltételek darabolása és letolása (minél előbb szűrjünk)
- Projekciók letolása (projektáljunk minél előbb)
- Utolsó lépésként kifejezések helyettesítése természetes összekapcsolással, -összekapcsolással.
Ha diszjunkciók is megjelennek, azok nehezíthetik a lekérdezések optimalizációját.
Bevezetés az SQL-be
Az SQL magas szintű programozási nyelv.
Az adatbázis-kezelő rendszer kitalálja a leggyorsabb végrehajtási módot.
SELECT -- az érdekes attribútumok
FROM -- egy vagy több tábla
WHERE -- a táblák soraira vonatkozó feltételek
AS -- átnevezés
LIKE -- mintaillesztés
IN -- eleme
A lekérdezés jelentése
- Kezdjük a
FROMzáradékban megadott relációval. - Alkalmazzuk a
WHEREzáradékban megadott kiválasztási feltételt. - Levetítjük az eredményt a
SELECTzáradékban megadott oszlopokra.
A SELECT záradékban megjelenhet algebrai kifejezés, például:
SELECT teázó, tea, ár*114 AS árJenben
FROM Felszolgál
Információ integráció
- Sokszor az adatbázisokat sok forrásból építik fel (adattárházak).
- Tegyük fel, hogy minden teázónak van egy saját Menü(tea, ár) táblája.
- A Felszolgál(teázó, tea, ár) tábla elkészítéséhez minden ilyen táblát fel kell dolgoznunk és a teázó nevét konstansként kell beszúrnunk.
Például Joe teázója esetében ezzel a lekérdezéssel dolgozhatunk:
SELECT ’Joe teázója’, tea, ár
FROM Menü;
A WHERE zárdékában logikai kifejezéseket is használhatunk.
Minták
A feltételekben a sztringeket mintákra illeszthetjük a LIKE kulcsszóval.
Minta aposztrófok közötti szöveg az alábbi jelekkel: % = “akármennyi karakter”; _ = “tetszőleges karakter, pontosan egy.”
Például:
SELECT név
FROM Vendégek
WHERE cím LIKE '%Budapest%';
NULL összehasonlítás
Az SQL valójában 3-értékű logikát használ: TRUE, FALSE, UNKNOWN.
Ha egy értéket (NULL értéket is beleértve) NULL-lal
hasonlítunk, az eredmény UNKNOWN.
Egy sor akkor és csak akkor kerül be az eredménybe,
ha a WHERE záradék TRUE értéket ad.
Többrelációs lekérdezések
Általában több táblából kell kinyernünk az adatokat.
Ekkor a relációkat a FROM záradékban kell felsorolnunk.
Az azonos attribútum neveket az alábbi módon különböztetjük meg egymástól:
<reláció>.<attribútum> .
Példa:
SELECT tea
FROM Szeret, Látogat
WHERE teázó = 'Joe teázója' AND
Látogat.vendég = Szeret.vendég
Szemantika
Formális szemantika
Majdnem ugyanaz, mint korábban:
- Vegyük a
FROMzáradékban szereplő relációk Descartes-szorzatát. - Alkalmazzuk a
WHEREzáradék feltételét. - Vetítsünk a
SELECTzáradék oszlopaira.
Operációs szemantika
Képzeljük úgy, mintha minden FROM záradékbeli táblához tartozna
egy sorváltozó.
- Ezekkel a sorok összes lehetséges kombinációját vesszük.
- Ha a sorváltozók a
WHEREzáradékot kielégítő sorra mutatnak, küldjük el ezeket a sorokat aSELECTzáradékba.
Explicit sorváltozók
Esetenként egy tábla több példányára is szükségünk van.
- A
FROMzáradékban a relációk neve után adjuk meg a hozzájuk tartozó sorváltozók nevét. - Egy relációt mindig átnevezhetünk ily módon, akkor is, ha egyébként nincs rá szükség.
Példa: önmagával vett összekapcsolás
SELECT b1.név, b2.név
FROM Teák b1, Teák b2
WHERE b1.gyártó = b2.gyártó AND
b1.név < b2.név;
Alkérdések
A FROM és WHERE záradékban zárójelezett
SELECT-FROM-WHERE utasításokat (alkérdés) is
használhatunk.
Példa: a FROM záradékban a létező relációk
mellett, alkérdéssel létrehozott ideiglenes táblát is
megadhatunk.
- Ilyenkor a legtöbb esetben explicite meg kell adnunk a sorváltozó nevét.
SELECT tea
FROM Szeret, (SELECT vendég
FROM Látogat
WHERE teázó = 'Joe teázója')JD
WHERE Szeret.vendég = JD.vendég;
Az IN művelet
<sor> IN (<alkérdés>)igaz, akkor és csak akkor, ha a sor eleme az alkérdés eredményének.- Tagadás:
<sor> NOT IN (<alkérdés>). - Az
IN-kifejezések aWHEREzáradékban jelenhetnek meg.
Példa:
SELECT *
FROM Teák
WHERE név IN (SELECT tea
FROM Szeret
WHERE vendég = 'Fred');
Források
- Diasor - Relációs algebra lekérdezések optimizációja
- Diasor - SQL bevezetés I - pdf
- Diasor - SQL bevezetés II - pdf
SQL Bevezetés folytatás, haladó SQL
Bevezetés az SQL-be II
Az EXIST művelet
EXIST(<alkérdés>) akkor és csak akkor igaz, ha az alkérdés eredménye nem üres.
SELECT *
FROM Teák b1
WHERE NOT EXISTS (
SELECT *
FROM Teák
WHERE gyártó = b1.gyártó AND
név != b1.név
);
Az ANY művelet
x = ANY(<alkérdés>) akkor és csak akkor igaz, ha x egyenlő az alkérdés legalább egy sorával
Az ALL művelet
x != ALL(<alkérdés>) akkor és csak akkor igaz, ha x az alkérdés egyetlen sorával sem egyezik meg.
SELECT tea
FROM Felszolgál
WHERE ár >= ALL(
SELECT ár
FROM Felszolgál
);
Unió, metszet, különbség
(<alkérdés>)UNION/INTERSECT/MINUS(<alkérdés>)
(SELECT * FROM Szeret)
INTERSECT
(
SELECT vendég, tea
FROM Felszolgál, Látogat
WHERE Felszolgál.teázó = Látogat.teázó
);
A SELECT-FROM-WHERE multihalmaz szemantikát használnak, a halmazműveleteknél mégis a halmaz szemantika érvényes.
Ismétlődések kiküszöbölése
DISTINCT kulcsszó.
Összekapcsolás kifejezések
Az SQL-ben számos változata megtalálható az összekapcsolásnak.
Ezek a kifejezések önmagukban is állhatnak lekérdezésként, vagy a FROM zátadékban is megjelenhetnek.
Descartes szorzat és természetes összekapcsolás:
R NATURAL JOIN S
R CROSS JOIN S
Theta összekapcsolás
R JOIN S ON <feltétel>
Vendégek JOIN Látogat ON
név = vendég;
Relációs algebra és az SQL
Relációs algebra: érdekes a "hogyan" kérdés is
Kapcsolat a relációs algebra műveletek és SQL záradékok, kulcsszavak között.
SQL-nél mondtuk: "hogyan" helyett "mit"
DBMS kitalálja a leggyorsabb végrehajtási módot, háttérben optimalizál
Van a relációs kalkulus, amely deklaratív nyelv.
Haladó SQL
Összekapcsolás típusok
- Descartes-szorzat
- Belső összekapcsolás
- Külső összekapcsolás
Belső összekapcsolások
- Természetes összekapcsolás
- Theta összekapcsolás
- Félig összekapcsolás (semi join)
- Anti összekapcsolés
Külső összekapcsolás
Kiterjesztett relációs algebra
Összekapcsoljuk és relációkat
Három különböző művelet
azon sorait, melyeknek nincs beli párja lógó soroknak nevezzük
A külső összekapcsolás megőrzi a lógó sorokat NULL értékrkkel helyettesítve a hiányzó értékeket.
Összesítések
SUM, AVG, COUNT, MIN, MAX összesítő függvények a SELECT záradékában alkalmazhatjuk egy-egy oszlopra.
COUNT(*) az eredmény sorainak számát adja meg.
SELECT AVG(ár)
FROM Felszolgál
WHERE tea = 'Brisk';
SELECT COUNT(DISTINCT ár)
FROM Felszolgál
WHERE tea = 'Brisk';
NULL értékek nem számítanak az összesítésben.
NULLsoha nem számít aSUM, AVG, COUNT, MIN, MAXfüggvények kiértékelésekor.- De ha nincs
NULLértéktől különböző érték az oszlopban, akkor az összesítés eredményeNULL- kivéve a
COUNT, ami az üreshalmazon -t ad vissza.
- kivéve a
Csoportosítás
Egy kifejezést GROUP BY záradékkal folytathatjuk, melyet attribútomok listája követ.
SELECT tea, AVG(ár)
FROM Felszolgál
GROUP BY tea;
A GROUP BY záradékot egy HAVING <feltétel> záradék követheti, ami a már csoportokat szűri.
SELECT tea, AVG(ár)
FROM Felszolgál
GROUP BY tea
HAVING COUNT(teázó) >= 3 OR
tea IN (
SELECT név
FROM Teák
WHERE gyártó = 'Pete'
);
Adatbázis módosítások
A módosító utasítások nem adnak eredményt, hamen az adatbázist változtatják meg.
3-féle módosító létezik:
INSERTDELETEUPDATE
Ezek a Data manipulation Language része.
Beszúrás
Ha egyetlen sort szúrunk be:
INSERT INTO <reláció>
VALUES (<attribútum lista>);
A reláció után megadhatjuk az attribútumait, mert nem emlékszünk az attribútum sorrendre, vagy nincs minden attribútumnak
értéke, és szeretnénk, ha a hiányzó értékeket NULL vagy default értékkel helyettesítenénk.
Default értékek megadása
A CREATE TABLE utasításban van rá lehetőség
CREATE TABLE Vendégek (
név CHAR(30) PRIMARY KEY,
cím CHAR(50) DEFAULT '123 Sesame St.'
telefon CHAR(16)
);
Több sor beszúrása
Egy lekérdezés eredményét is beszúrhatjuk a következő módon:
INSERT INTO <reláció> (<alkérdés>);
Törlés
DELETE FRPM <reláció>
WHERE <feltétel>;
Itt is van lehetőség több sort töröni allekérdezéssel.
Törlés szemantikája: Elősször kijelölünk, aztán törlünk.
Módosítás
UPDATE <reláció>
SET <attribútum értékadások listája>
WHERE <sorokra vonatkozó feltétel>;
Adatbázis sémák SQL-ben
A Data Definition Language segítségével hozhatunk létre adatobjektumokat, deklarálhatunk megszorításokat.
Relációk létrehozása
CREATE TABLE <név> (
<elemek listája>
);
Legfontosabb típusok:
INTFLOATCHAR(n): rögzített hosszVARCHAR(n): legfeljebb hosszúságDATETIME
Kulcsok megadása
Egy attribútomot vagy attribútum listát kulcsként deklarálhatunk (PRIMARY KEY vagy UNIQUE)
Minden formája a megszorításnak azt követeli meg, hogy relációnak ne legyen két olyan sora, melyek megegyeznek a kulcs attribútumokon.
CREATE TABLE Felszolgál (
teázó CHAR(20),
tea VARCHAR(20),
ár REAL,
PRIMARY KEY (teázó, tea)
);
PRIMARY KEY vs UNIQUE
- Egy relációhoz egyetlen
PRIMARY KEYtartozhat és többUNINQUEmegszorítás. - A
PRIMARY KEYegyetlen attribútuma sem kaphatNULLértéket. AUNIQUEmegszorításnál szerepelhetnekNULLértékek egy soron belül akár több is.
Relációk törlése
DROP TABLE <név>
Források
Megszorítások, tranzakciók, nézettáblák, indexek, jogosultságok
Megszorítások és triggerek
A megszorítás adatelemek közötti kapcsolat, amelyet az AB rendszernek fent kell tartania.
Triggerek olyankor hajtódnak végre, amikor valamilyen esemény történik, mint pl. sorok beszúrása egy táblába.
Megszorítások típusai:
- Kulcsok
- Idegen kulcsok, vagy hivatkozási épség megszorítás
- Attribútum alaú megszorítás: egy adott attribútum lehetséges értékeiről mond valamit
- Sor alapú megszorítás: mezők közötti kapcsolat leírása
- Globális megszortás: bármilyen SQL kifejezés
Idegen kulcsok
Egy reláció attribútumainak értékei egy másik reláció értékei között is meg kell, hogy jelenjenek együttsesn.
A REFERENCES kulcsszót kell használni:
- egy attribútum után
- A séma elemenként:
FOREIGN KEY (<attribútumok listája>)
REFERENCES<reláció>(<attribútumok>)
A hivatkozott attribútumoknak kulcsnak kell lenniük.
Reláció sérülés
Egy idegen kulcs megszorítás relációról relációra kétféleképpen sérülhet:
- Egy -be történő beszúrásnál -ben nem szereplő értéket adunk meg
- Egy -beli törlés "lógó" sorokat eredményez -ben
Hogyan védekezhetünk?
- Default
- Továbbgyűrűzés
- Set
NULL
-
Ha egy idegen kulcsot deklarálunk megadhatjuk a
SET, NULL, CASCADEstratégiát is módosításra és törlésre egyaránt. -
Az idegen kulcs deklarálása után ezt kell írnunk:
ON[UPDATE, DELETE][SET NULL, CASCADE] -
Ha ezt nem adjuk meg, a default stratégia működik.
Attribútum alapú ellenőrzések
- Adott oszlop értékeire vonatkozóan
- A
CHECK(<feltétel>)hozzáadása az attribútum deklarációjához - Feltételben csak az adott attribútum neve, más attribútumok csak alkérésben
- Csak beszúrásnál és módosításnál hajtódik végre az attribútum alapú ellenőrzés
Sor alapú megszorítások
CHECK(<feltétel>)megszorítás a séma elemeként- Feltételben tetszőleges oszlop és reláció (más relációk attribútumai csak alkérésben)
- Csak beszúrásnál és módosításnál ellenőrzi a rendszer
Globális megszorítás
- Adatbázissémához tartoznak
CREATE ASSERTION <név>
CHECK(<feltétel>);
- Bármilyen módosításra ellenőriz
- Egy okos rendszer felismeri, hogy mely változtatásokra szükséges ez valóban
Triggerek
-
A globális megszorításokkal sok mindent le lehet írni, de ellenőrzésük gondot jelenthet.
-
Az attribútum- és sor-alapú megszorítások ellenőrzése egyszerűbb,de ezekkel nem tudunk mindent kifejezni.
-
A triggerek esetén a felhasználó mondja meg, hogy egy megszorítás mikor kerüljön ellenőrzésre.
-
A triggereket eseményenként ECA szabályoknak (event-condition-action) is nevezik.
Példa:
CREATE TRIGGER TeaTrig
BEFORE INSERT ON Felszolgál
REFERENCING NEW ROW AS ÚjSor
FOR EACH ROW
WHEN (ÚjSor.tea NOT IN
(SELECT név FROM Teák))
INSERT INTO Teák(név)
VALUES(ÚjSor.tea);
Tranzakciók
- Olyan folyamat, ami adatbázis lekérdezéseket, módosításokat tartalmaz
- Az itasítások egy "értelmes egészet" alkotnak
- Egyetlen utasítást tartalmaznak, vagy SQL-ben eyplicit módon megadhatóak
- Kell: végrehajtásuk tartós legyen
- Az oprendszerektől eltérően az AB rendszereknek el kell különíteniük a folyamatokat
Tranzakciók feldolgozása
A tranzakciófeldolgozó két nagyobb részből áll:
- Konkurenciakezelő: tranzakciók oszthatatlanságára, elkülönítésére
- Naplózás- és helyreállítás-kezelő: tranzakciók tartóssága
ACID tranzakciók
- Atomiság (atomicity): vagy az összes, vagy egy utasítás sem hajtódik végre
- Konzisztencia (consistency): az adatbázis megszorítások megőrződnek
- Elkülönítés (isolation): a felhasználók számára úgy tűnik, mintha a folyamatok elkülönítve, egymás után futnának le.
- Tartósság (durability): egy befejeződott tranzakció módosítási nem vesznek el.
COMMIT
- A
COMMITSQL utasítás végrehajtása után a tranzakció véglegesnek tekinthető. - A tranzakció módosításai véglegesítődnek
ROLLBACK
- A
ROLLBACKSQL utasítás esetén a tranzakció abortál, azaz az összes utasítás visszagörgetésre kerül. - A 0-val való osztás bvagy egyéb hibák szintén okozhatnak rollback-et.
Elkülönítési szintek
- Az SQL négy elkülönítési szintet definiál, amelyek megmondják, hogy milyen interakciók engedélyezettek egy időben végrehajtandó tranzakciók közöt.
- Ezek közül az egyik szint ("sorbarendezhető") = ACID tranzakciók.
- Minden AB rendszer a saját tetszése szerint implementálhatja a tranzakciókat.
SET TRANSACTION ISOLATION LEVEL X, ahol X =
SERIALIZABLE: ACID tranzakcióREPEATABLE READ: ha az adatot újra beolvassuk, akkor amit először láttunk, másodszor is látni fogjukREAD COMMITED: a tranzakció csak kommitálás utáni adatot láthat, de nem feltétlenül mindig ugyan azt az adatotREAD UNCOMMITED: akkor is látja a tranzakció az adatokat, amikor a változtatások még nem lettek véglegesítve

Nézettáblák
-
A nézettábla olyan reláció, amit tárolt táblák és más nézettáblák felhasználásával definiálunk.
-
Kétféle létezik:
- virtuális: nem tárolódik az adatbázisban, csak a relációt megadó lekérdezést tárolunk.
- materializált: kiszámítódik, majd tárolásra kerül
-
Deklaráció:
CREATE [MATERIALIZED] VIEW <név> AS <lekérdezés>;
- Alapesetben virtualizált nézettábla jön létre.
Materializált nézettáblák
-
Probléma: minden alkalommal, amikor az alaptáblák valamelyike változik, a materializált nézettábla frissítése is szükségessé válhat, ez viszont néha túl költséges.
-
Megoldás: Periodikus frissítése a materializált nézettáblának, amelyek egyébként "nem aktuálisak".
Indexek
-
Index = olyan adatszerkezet, amivel egy-egy reláció sorait gyorsabban érhetjük el adott attribútumának értéke, attribútumainak értékei alapján.
-
Lehet hash tábla, de az AB rendszerekben a legtöbb esetben kiegyensúlyozott keresési fával valósítják meg (B-fák)
-
Nincs tipikus megadás, de tipikus szintaxis:
CREATE INDEX TeaInd ON Teák(gyártó);
CREATE INDEX EladásInd ON Felszolgál(teázó, tea);
- Adott értékre az index azokhoz a sorokhoz irányít, ahol ez a érték megjelenik a megfelelő attribútumoknál.
Adatbázisok hangolása
- Az adatbázisok hangolásánál komoly kérdést jelent annak eldöntése, hogy milyen indexeket használjanak.
- Mellette: az index felgyorsíthatja a lekérdezések végrehajtását
- Ellene: a módosítások lassabbak lesznek, hiszen az indexeket is módosítani kell.
Jogosultságok
- AZ SQL-ben több fajta jogosultság és adatobjektum létezik, mint egy tipikus fájlrendszerben.
- Összességében 9 jogosultság, ezek némelyike egy reláció egyetlen attribútumára is megadható.
Legfontosabb jogosultságok:
-
SELECT -
INSERT -
UPDATE -
DELETE -
A magunk lkészítette objektumok esetében az összes jogosultsággal rendelkezünk
-
Másoknak is megadhatunk jogosultságokat
GRANT <jogosultságok listája>
ON <adatobjektum>
TO <jogosuétsági azonosítók listája>
- A
WITH GRANT OPTIONutasításrész lehetővé teszi, hogy aki megkapta a jogosultságot, tovább is adhassa azt.
Visszavonás:
REVOKE <jogosultságok listája>
ON <adatobjektum>
TO <jogosuétsági azonosítók listája>
- Az általunk kiadott jogosultságok ez által visszavonódnak, de ha máshonnan is megkapták ugyanazt a jogosultságot, akkor az még megmarad.
REVOKE opciói:
CASCADE: azok a jogosultságok is visszavonódnak, amelyeket az a személy adott ki, akitől most megvonjuk.RESTRICT: a visszavonás nem hajtódik végre, amíg a visszavonandó jogosultságtól függő jogosultságok is vannak.
Jogosultsági azonosítók
- A felhasználókat egy jogosultsági azonosító alapján azonosítunk, általában ez a bejelentkezési név.
- Külön jogosultságok azonosító a
PUBLIC
Források
- Diasor - Megszorítások
- Diasor - Tranzakciók, nézettáblák, indexek I.
- Diasor - Tranzakciók, nézettáblák, indexek II.
- Diasor - Jogosultságok
Adatbázis tervezés
A relációs adatmodell tervezése
-
Megtehetnénk, hogy valamennyi adatot egyetlen relációba tennénk:
- A felhasználó szempontjából kényelmes
- Sok "felesleges" adat van benne nem jó tárolási hatékonyság, az adatbázist ellentmondásossá teheti
-
valahogy a felhasználási eset fogalmait, kapcsolatait modellezni kell
-
De még így is előfordulhat, hogy nem lesz elég "ügyes" a modellezés még mindig lehetnek felesleges adatok konkrét előfordulásnál.
-
Redundancia:
- Adott egy reláció. Ha valamely attribútum értékét ki tudjuk az attribútumok értékeiből "következtetni" a relációt redundásnak nevezzük
Funkcionális függőségek
egy relációra vonatkozó megszorítás, miszerint ha két sor megegyezik összes attribútumán, attribútumain is megg kell, hogy egyezenek.
- Jelölés: attribútom halmazokat, attribútumokat jelöl.
- Jelölés: attribútum halmaz helyett -t írunk.
Jobboldalak szétvágása / dekompozíció
- akkor és csak akkor teljesül relációra, ha is teljesül -en
- Baloldalak szétvágására nincs általános szabály
- Általában funkcionális feltételek jobboldalán egyetlen attribútum szerepel majd
Relációk kulcsai
- szuperkulcs relációra, ha funkcionálisan meghatározza attribútumait.
- kulcs -en, ha szuperkulcs, de egyetlen valódi részhalmaza sem szuperkulcs.
Armstrong axiómák I
- (A1) Reflexivitás: ha , akkor . Az ilyen függőségeket triviális függőségnek nevezzük.
- (A2) Bővítés: ha teljesül, akkor tetszőleges -ra teljesül
- (A3) Tranzitivitás: ha és , akkor
Lezárás
- Adott funkcionális függőségeknek egy halmaza: bizonyos attribútumértékből esetleg milyen más attribútum értékeket kephatunk?
- Adott reláció és funkcionális függőségek egy halmaza mellett, lezártja: jelölésben az összes olyan attribútum halmaza, amira következik -ből
Algoritmus
- Kiindulás:
- Indukció: Olyan funkcionális függőségeket keresünk, melyeknek a baloldalára már benne van -ban. Ha ilyen, -t hozzáadjuk -hoz.
- Ha -hoz már nem lehet további attribútumot adni vége.
Ez az algoritmus helyes, azaz tényleg -t számítja ki.
Az összes következmény funkcionális függőség megtalálása
-
Motiváció: "normalizálás", melynek során egy relációsémát több sémára bonthatunk szét.
-
Alapötlet:
- Induljunk ki a megadott funkcionális függőségekből és keressük meg az összes nem triviális funkcionális függőséget, ami a megadott funkcionális függőségekből következik.
- Csak azokkal a funkcionális függőségekkel foglalkozunk, amelyekben a projektált séma attribútumai szerepelnek
-
Exponenciális algoritmus:
- Minden attribútumhalmazra számítsuk ki -t
- Asjuk hozzá a függőségeinkhez -t minden -ra -ből
- Dobjuk ki -t, ha is teljesül, mert az -ból minden esetben következik.
- Végül csak azokat a funkcionális függőségeket használjuk, amelyekben csak a projektált attribútumok szerepelnek.
Források
Adatbázis tervezés II
- Cél: az anomáliák és a redundancia megszüntetése
- Módosítási anomália
- Törlési anomália
- Beszúrási anomália
Relációk felbontása
relációt, attribútumokkal helyettesítsük és relácciókkal úgy, hogy
Veszteségmentes felbontás
-
Ha teljesül, akkor az előbbi összekapcsolásra azt mondjuk, hogy veszteségmentes. Itt egy sémájú relációt jelöl és attribútumainak részhalmazai az
-
jelentése: sorai az attribútumaira projektálva.
-
Látható, hogy mindig teljesül.
Boyce Codd normálforma
reláció BCNF normálformában van, ha minden nemtriviális funkciónális függőségre -ben szuperkulcs.
- Nemtriviális: nem része -nek
- Szuperkulcs: tartalmaz kulcsot (ő maga is lehet kulcs)
BCNF-re bontás:
- Adott reláció ls funkcionális függőségek.
- Van-e olyan ami sérti a BCNF-t?
- Ha van olyan következmény -ben, ami sérti a BCNF-t, akkor -beli funkcionális függőség is sérti
- Kiszámoljuk -t:
- Ha itt nem szerepel az összes attribútum, nem szuperkulcs
- dekomponálása felhasználásával:
- -t helyettesítsük az alábbiakkal:
- Projektáljuk a megfelelő -beli FF-eket a két új relációsémára
- -t helyettesítsük az alábbiakkal:
Miért működik a BCNF?
- esetén ha egy veszteségmentes felbontás, pedig veszteségmentes felbontása, akkor is veszteségmentes felbontás.
- Könnyen ellenőrizhrtő, hogy BCNF felbontás dián az veszteségmentes.
- Minden két attribútum séma BCNF normálformában van
- A fentiekkel igazolható:
- Az algoritmus valóban veszteségmentes felbontást ad, ám sajnos exponenciális lépésszámú is lehet a függődégek vetítése miatt.
Chase teszt veszteségmentességhez
Az -beli függőségeket használva egyenlővé tesszük azokat a szimbólumokat, amelyeknek ugyanazoknak kell lennie, hogy valamelyik függőség ne sérüljön.
- Ha a két egyenlővé teendő szimbólum közül az egyik index nélküli, akkor a másik is ezt az értéket kapja.
- Két indexes szimbólum esetén a kisebbik indexű értéket kapja meg a másik.
- A szimbólumok minden előfordulását helyettesíteni kell az új értékkel. Az algoritmus véget ér, ha valamelyik sor -vel lesz egyenlő, vagy több szimbólumot már nem tudunk egyenlővé tenni.
Ha szerepel a tablóban, akkor valóban -nek egy sora, és mivel -t tetszőlegesen választottuk, ezért a felbontás veszteségmentes.
Ha nem kapjuk meg -t, akkor viszont a felbontás nem veszteségmentes.
A harmadik normálforma
Motiváció
- Bizonyos FF halmazok esetén a felbontáskor elveszíthetünk függőségeket.
- és
- pl.:
- Két kulcs van: és
- megsérti a BCNF-t, tehát -re dekomponálunk
A probléma az, hogy és sémákkal nem tudjuk kikényszeríteni függőséget
3NF
-
3.normálformában (3NF) úgy módosul a BCNF feltétel, hogy az előbbi esetben nem kell dekomponálnunk.
-
Egy attribútum prím (elsődleges attribútum), ha legalább egy kulcsnak eleme.
-
nem-triviális FF, megsérti 3NF-t akkor és csak akkor, ha nem szuperkulcs és nem prím.
-
minden nem triviális függőségre igaz, hogy bal oldala szuperkulcs, vagy jobb oldala csak elsődleges attribútumokat tartalmaz
-
3NF feltétel és a BCNF feltétel közötti különbség a "vagy jobb oldala csak elsődleges attribútumokat tartalmaz"
3NF-re bontás
Minimális bázis létrehozása
- Jobb oldalak szétvágása.
- Próbáljuk törölni az FF-eket egymás után. Ha a megmaradó FF-halmaz nem ekvivalens az eredetivel, akkor nem törölhető az épp aktuális FF.
- Egymás után próbáljuk csökkenteni a baloldalakat, és megnézzük, hogy az eredetivel ekvivalens FF-halmazt kapunk-e.
A minimális bázis minden FF-re megad egy sémát a felbontásban.
- A séma a jobb- és baloldalak uniója lesz ( FF, séma) .
- Ha a minimális bázis FF-jei által meghatározott sémák ( FF, séma) között nincs szuperkulcs, akkor hozzáadunk a felbontáshoz egy olyan sémát, amely maga egy kulcs az relációra.
3NF vs BCNF
A dekompozícióknak három fontos tulajdonsága lehet:
- Veszteségmentes összekapcsolás (információ visszaállíthatóság)
- Függőségek megőrzése
- Anomáliák kiküszöbölése
Az (1) tulajdonság teljesül a BCNF esetében.
-
A 3NF (1) és (2)-t is teljesíti, de maradhat benne anomália (általában ez nem akkora baj)
-
A BCNF esetén (2) sérülhet, viszont (FF-ek okozta) anomália nem lehet benne
Források
Többértékű függőségek, egyed kapcsolat modell
Többértékű függőségek
A többértékű függőség: az reláció fölött teljesül, ha bármely két sorra, amelyek megegyeznek az minden attribútumán, az attribútumaihoz tartozó értékek felcserélhetők, azaz a keletkező két új sor -beli lesz.
Más szavakkal: minden értéke esetén az -hoz tartozó értékek függetlenek az értékeitől.
Többértékű függőség szabályok
-
Minden funkcionális függőség egyben többértékű függőség is.
- Ha és két sor megegyezik -en, -on is megegyezik, emiatt ha ezeket felcseréljük, az eredeti sorokat kapjuk vissza, azaz:
-
Komplementálás: Ha és jelöli az összes többi attrubútum halmazát, akkor
-
Ugyanúgy, mint az FF-ek esetében, a baloldalakat nem "bánthatjuk" általában.
-
Az FF-ek esetében a jobboldalakat felbonthattuk, míg ebben az esetben ez sem tehető meg.
Negyedik normálforma
- A TÉF-ek okozta redundanciát a BCNF nem szünteti meg.
- Megoldás: a negyedik normálforma
- A negyedik normálformánál amikor dekomponálunk, a TÉF-eket úgy kezeljük, mint az FF-eket, a kulcsok megtalálásánál azonban nem számítanak.
Triviális TÉFek
Legyen egy reláció, és részhalmazai attribútumainak, jelölés:
- TÉF automatikusan fennáll, ha
- TÉF automatikusan fennáll, ha
4NF definíció
Egy reláció 4NF-ben van, ha minden nemtriviális TÉF esetén szuperkulcs
- Nemtriviális TÉF:
- nem részhalmaza -nek
- és együtt nem adják ki az összes attribútumot.
- A szuperkulcs definíciója ugyanaz marad, azaz csak az FF-ektől függ.
BCNF vs 4NF
- Kiderült, hogy minden FF TÉF is.
- Így ha 4NF-ben van, akkor BCNF-ben is.
- De lehet úgy BCNF-ben, hogy közben nincs 4NF-ben.
Dekompozíció és 4NF
Ha megsérti a 4NF-t, akkor -t hasonlóan dekomponáljuk, mint a BCNF esetén.
- az egyik dekomponált reláció
- Az -be nem tartozó attribútumok a másik.
TÉF és FFek együttes következtetése
- Probléma: relációsémához adott a TÉF-ek és FF-ek egy halmaza, kérdés: egy adott FF vagy TÉF következik-e ezekből fölött?
- Megoldás: használjunk egy táblázatot (tablót), hogy a függőségek hatásait feltárjuk. (A chase mögötti ötletet terjesztjük ki.)
Miért foglalkozunk ilyesmivel?
- 4NF azon múlik, hogy van-e olyan TÉF, ami sérti a feltételt.
- Előfordulhat, hogy a megadott FF-ek és TÉF-ek nem sértik a feltételt, de egy belőlük következő függőség igen.
- Amikor dekomponálunk az FF-eket és TÉF-eket is vetítenünk kell.
Következtetés
FF használata
FF alkalmazásánál keressük meg azon sorpárokat, amelyek megegyeznek attribútumain. Az attribútumain is tegyük őket egyenlővé.
- Egy változót egy másikra cseréljünk.
- Ha a lecserélt változó a célsorban is megjelenik, ott is cseréljünk.
TÉF használata
Egy TÉF használatánál keressünk két sort, amelyek megegyeznek X attribútumain.
- Adjuk hozzá a tablóhoz azokat a sorokat, amelyeket az attribútumaihoz tartozó értékek felcserélésével kapunk.
Célok
-
Az ellenőrzésekor akkor nyertünk, ha a megfelelő változók -hez tartozó minden oszlopban egyenlőek.
-
akkor győztünk, ha sikerül egy olyan sort kigenerálni, ami az eredeti két sorból keletkezik értékeinek felcserélésével.
Végjáték
- Használjuk az összes FF-et és TÉF-et, amíg bármiféle változtatás történhet.
- Ha nyertünk, nyertünk.
- Ha nem, egy ellenpéldát kaptunk.
- A kapott előfordulás az összes előre megadott függőséget teljesíti.
- Az eredeti két sor megsérti a kikövetkeztetendő függőséget.
TÉFek vetítése
- Le kell tudnunk vetíteni megadott függőségeket 2 reláció sémára
- Legrosszabb eset: ki kell próbálnunk minden lehetséges FF-et és TÉF-et a felbontott relációkra
- Chase teszt alkalmazása; Cél egy TÉF ellenőrzésénél: olyan sor előállítása a tablóban, amely indexeletlen betűket tartalmaz a felbontott reláció oszlopaira
Egyed kapcsolat modell
- Egyed kapcsolat modellekkel adatbázissémát vázolhatunk fel.
- A főbb részek felvázolásával hatékonyabb lehet egy működő adatbázist.
Egyedhalmazok
- Egyed (entity)
- Egyedhalmaz
- Az objektum-orientált nyelvek osztály fogalmához hasonló
- Attribútum
- Atomi értékűek, nem rekordok, tömbök
Diagrammok
- Az egyed kapcsolat diagramban:
- egyedhalmaz: téglalap
- alosztályok: háromszög (nincs töbszörös öröklés)
- attribútum: ovális
- kulcs(ok): aláhúzás
- sok-sok, sok-egy, egy-egy kapcsolat (rombusz)
- kapcsolathalmaz
- ezek össze vannak kötve
- egyedhalmaz: téglalap
Források
Egyed-kapcsolat modell befejezése, objektum-relációs adatbázisok elkezdése
Egyed-kapcsolat tervezési technikák
- Redundancia elkerülése
- helypazarlás
- növeli az inkonzisztencia veszélyét
- A gyenge egyedhalmazok óvatos használata
- jobb lehetőség lehet egyedi azonosítókat bevezetni (pl.: rendszám)
- amikor ez nem lehetséges, akkor érdemes gyenge egyedhalmazokhoz fordulni
- Ne használjunk egyedhalmazt, ha egy attribútum éppúgy megfelelne a célnak
- egy egyedhalmaznak többnek kell lennie mint egy egyszerű név, vagy tulajdonság, azaz legalább egy nem kulcs attribútumának kell lennie.
- Vagy a "sok" végén szerepel egy sok-egy kapcsolatnak
Egyed-kapcsolat diagramok átírása relációsémává
- Egyedhalmaz reláció
- Attribútumok attribútumok
- relációk összevonhatók, ha
- Az egyedhalmazból kapott reláció
- valamint azon sok-egy kapcsolatok relációi, melyeknél az a "sok" oldalon szerepel
- Egy gyenge egyedhalmazból kapott relációnak a teljes kulcsot tartalmaznia kell, valamint a saját, további attribútumokat.
- A támogató kapcsolatot nem írjuk át, redundancióhoz vezetne.
- Kapcsolat relációk, melyeknek az attribútumai csak:
- az összekapcsolt egyedhalmazok kulcs-attribútumai
- és a kapcsolat attribútumait tartalmazzák
- Egyed alosztályok
- objektumorientált
- a "szülő" attribútumait is tároljuk az alosztályban
- pl.: Teák(név, gyártó) Gyógyteák(név, gyártó, szín)
- null értékek használata
- minden attribútumot tárolunk, de csak egy reláció van
- ami az adott egyedre nem releváns, oda
NULLértéket helyezünk
- E/K style
- pl.: Teák(név, gyártó), Gyógyteák(név, szín)
Objektum-relációs adatbázisok
Relációs és O-O modell egyesítése
- Az O-O modell több érdekes adattípust támogat - nem csak egyszerű állományokat
- A relációs modell magas szintű lekérdezéseket támogat
- Objektum-relációs adatmodell egy olyan kísérlet, amely mindkét világból a legjobbat szeretné nyújtani
Reláció objektumreláció
- A reláció alapvető fogalom marad, de
- Attribútumokhoz szerkesztett struktúrált típusok
- Metódusok
- Sorok azonosítói
- Hivatkozások
Beágyazott relációk
- Egy reláció attribútumának típusa nem csak atomi típus lehet, hanem pl. egy relációséma is
- Rekurzív definíció
- Kiindulás: atomi típus
- Indukció: reláció típusa séma egy vagy több attribútumnévvel és hozzátartozó típussal, az utóbbi lehet séma is
- Az atomi típusokat általában nem jelöljük külön, de a séma
típusú attribútumot annak nevével és zárójelben a sémához
tartozó attribútumok zárójelezett listájával adjuk meg
- Pl. Rel1(Attr1, Attr2(Attr2A, Attr2B), Attr3), ahol Attr2(Attr2A, Attr2B) egy relációséma
Források
9. Objektum-relációs adatbázisok
Hivatkozások
- Kell, hogy egy objektumra több hejről tudjunk hivatkozni annélkül, hogy többször eltárolnánk (redundancia csökkentése inkonzisztencia elkerülése).
- Újabb indukciós szabály: egy attribútum típusa egy adott sémájú sorra történő hivatkozás vagy adott sémájú sorokra történő hivatkozási halmaz is.
- Jelölés:
- ha attribútum típusa egy relációsémájú sorra történő hivatkozás
- ha attribútum tíousa egy séma soraira vonatkozó hivatkozási halmaz alakban jelenik meg.
Felhasználó által definiált adattípus
-
Egy O-O osztály definíciója, amely egy adatszerkezet és metódusai.
- Azonos "típusú" objektumok egy osztályt definiálnak
- Viselkedés: metódusok halmazával kifejezve, amelynek az osztályhoz tartozó objektumokon hajthatóak végre
-
Használati módok:
- Sortípus, vagyos egy reláció, mint adattípust kezelünk
- Egy reláció attribútumának a típusa
CREATE TYPE <typename>
AS OBJECT (<list of attribute pairs>);
Hivatkozások UDT-kre
- Ha egy UDT, akkor a -re történő hivatkozás típusa.
- Ezt OID-nek is hívják O-O rendszerekben
- Az OID élete végéig azonosít egy objektumot.
- Azonban az OID-től eltérően REF látható, bár általában nehezen értelmezhető.
UDT-k mint sortípusok
- Egy relációs táblát egy sortípus segítségével mint sémával lehet definiálni, az elemeinek felsorolása helyett.
CREATE TABLE <table name> OF <typename>;
UDT-k, mint oszloptípusok
- UDT lehet egy attribútum típusa
- Akár egy UDT deklarációban, vagy egy
CRATE TABLEutasításban, az UDT típus neve úgy használható mint az attribútum típusa.
Metódusok
- Az osztályok többek mint adatszerkezetek, lehetnek metódusaik.
- A metódusokat a
CREATE TYPE-ban deklaráljuk. - Definiálhatjuk a
CREATE TYPE BODYutasításban
CREATE TYPE BODY <typename> AS
<method definitions = PL/SQL method definitions, using "MEMBER FUNCTION" in place of "PROCEDURE">
END;
Rendező metódusok (ORACLE)
- Bármilyen UDT típusra bármelyik metódust rendező metódusnak deklarálhatjuk.
- A rendező metódusok visszatérő értéke <0, =0, vagy >0 lehet, ahogy a SELF objektumhoz viszonyítva az argumentum értéke <, =, vagy >
Példa:
CREATE TYPE BODY TeázóTípus AS
ORDER MEMBER FUNCTION
before(teázó2 TeázóTípus) RETURN INT IS
BEGIN
IF SELF.név < teázó2.név THEN RETURN –1;
ELSIF SELF.név = teázó2.név THEN RETURN 0;
ELSE RETURN 1;
END IF;
END;
END;
Oracle beágyazott táblák
- Megengedi, hogy a sorok egyes komponensei teljes relációk legyenek.
- Ha egy UDT, létrehozhatunk egy típust,
amelynek az értékei relációk, amelyeknek a
sortípusa viszont :
CREATE TYPE S AS TABLE OF T;
Beágyazott relációk eltárolása
- Oracle valójában nem tárolja el a beágyazott relációkat külön relációkként – még ha így is tűnik.
- Ehelyett, egy reláció van, amelyben egy attribútumra az összes beágyazott táblázatot és azok összes sorát eltárolja.
- Deklaráció a
CREATE TABLE-ben:NESTED TABLE A STORE AS R;
Források
XML séma
Félstruktúrált adat
- Fán alapuló adatmodell
- Motiváció: adatok rugalmas megjelenításe, dokumentumok megosztása rendszerek és adatbázisok között.
Gráf
- Pontok = objektumok.
- Az élek címkéi tulajdonképpen az attribútumnevek, kapcsolatok.
- Az atomi értékek a levelekben tárolódnak.
XML
- Extensible Markup Language
- A dokumentum deklarációval kezdődik, amit egy speciális
<?xml ... ?>tag határol. - Tagek: nyitó, záró, egymásba ágyazott tagek (case sensitive)
- Jól formált XML: megengedi, hogy önálló tageket vezessünk be.
- Nem hiányzik a deklaráció
- Minden nyitó tagnek megvan a záró párja
- Nincs átfedés az egymásba ágyazott tagek között
- Egyetlen gyökérelem van
- Valid XML: illeszkedik az előre megadott sémára: DTD vagy XML séma.
DTD felépítése
- Document Type Definition
<!DOCTYPE gyökér elem [
<!ELEMENT elem név(összetevők)>
. . . további elemek . . .
]>
-
ELEMENT: egy-egy elem leírása az elem nevét és zárójelek között az alelemek megadását jelenti. (sorrend, multiplicitás), a levelek (szöveges elemek) típusa (#PCDATA) -
Elem leírások:
- Az alelemek a felsorolás sorendjében kell, hogy kövessék egymást
- Egy elemet a felsorolásban egy további szimbólum követhet megadva a multiplicitást (*,+,?)
- A | szimbólum jelentése: vagy
-
Attribútumok:
- Az XML-ben a nyitó tag-ek mellett szerepelhetnek attribútumok.
- Egy DTD-ben,
<!ATTLIST E A1 type1 value1 A2 type2 value2...>az taghez tartozó attribútumokat adja meg. - Mindegyik attribútumhoz meg kell adni, hogy mi legyen a típusa, és mi legyen igaz az értékére.
-
ID és IDREF attribútumok:
- ID:
<E A = "xyz">- elem egy attribútuma, aminek típusa ID$ - IDREF: Egy $F$ elem az IDREF attribútum segítságável hivatkkozhat egy másik elemre annak ID attribútumán keresztül (IDREFS attribútummal tövvre is)
- ID:
XML séma felépítése
- Az XML sémák segítségével szintén XML dokumentumok szerkezetét adhatjuk meg. Itt több megszorítást lehet előírni, mint a DTD-k esetén.
- Az XML séma maga is egy XML dokumentum.
xs:element:name= a definiált elem nevetype= az elem típusa
- Lehyet XML séma típus, pl.: xs:string
- vagy egy olyan típus, amit az adott XML sémában deklaráltunk
- Összetett típusok:
- létehozás:
xs:complexType- a
nameattribútummal nevet adhatunk ennek a típusnak
- a
- az
xs:complexType`` egy tipikus aleleme azxs:sequence, amihezxs:element``` elemek egy sorozata tartozik
- létehozás:
xs:attribute:- elemek használatával az összetett tpuson belül a típushoz tartozó elemek attribűtumait adhatjuk meg
- az
xs::attributeelem attribútumai:nameéstypeuse = "required" | "optional"
- Elem megszorítások:
- az
xs:simpleTypesegítségével felsorolásokat adhatunk meg és az alaptípusra vonatkozó megszorításokat. nameattribútuma van ésxs:restrictionaleleme
- az
xs:restriction- a
baseattribútum adja meg, hogy melyik egyszerű típusra vonatkozik (pl.: xs:integer) {min, max}{Inclusive, Exclusive}a nény attribútum használatával alsó és felső korlátokat adhatunk meg.xs:enumerationalelem, avalueattribútum után megadhatjuk a felsorolás elemeit.
- a
- Kulcsok:
- Az
xs:elementelemhez tartozhatxs:keyalelem. - Jelentése: ezen az elemen belül, minden elem, ami egy adott szelektor ösvényen keresztül elérhető, egyedi értékekkel kell, hogy rendelkezzen a megadott mezőonek kombinációin (alelem, attribútum)
- Az
- Idegen kulcsok:
- A
xs:keyrefalelem azxs:elementelemen belül előírja, hogy ezen az elemen belül bizonyos értékek, melyeket ugyanúgy a szelektor és mezők használatával adhatunk meg, egy kulcs értékei között kell, hogy szerepeljenek.
- A
Keretrendszer
- Információintegráció: A különböző helyekről származó adatbázisokat úgy üzemeltetni, mintha egységes egészet alkotnának.
- Félig-strukturált adat: Viszonylag új adatmodell, amely segít megbirkózni az adatintegráció problémájával.
- XML: Szabványos nyelv a félig-strukturált adatok leírására.
Információintegrációs probléma
- Egymáshoz kapcsolható adatelemek sok helyen léteznek és elvileg együttműködésre alkalmasak volnának:
- De a különböző adatbázisok több tekintetben különböznek:
- Adatbázis modellek (relációs, objektum-orientált, NoSQL, dokumentum stb.)
- Séma (normalizált, nem normalizált)
- Szakkifejezések: tanácsadó alkalmazott-e? Visszavonult nyugdíjas-e? Alvállalkozó?
- Konvenciók (méter kontra láb [metrikus (SI, CGI), birodalmi].
Két megközelítés az integrációra
- Adattárház: Az adatforrásokról egy központi másolatot készít, és egy közös adat sémává transzformálja.
- Az adatokat naponta, hetente frissítik, de ennél nem szabad nagyobb pontosságot megcélozni.
- Mediáció, közvetítés: Az összes adatforrásra egy nézetet kell létrehozni, mintha egy integrált rendszer részei volnának:
- A nézetre vonatkozó lekérdezést úgy lehet megválaszolni, hogy a lekérdezést az egyes adatforrások szakkifejezéseire fordítják le és azután kérdezik le az eredeti adatforrásokat
Források
XML lekérdezőnyelvek
Az XPath/XQuery adatmodell
- A relációk megfelelője ebben a környezetben
- Ez azt jelenti, hogy a bemenetet, a köztes lépések eredményeit és a végeredményt is tételek listájaként kezeljük.
- Egy tétel lehet:
- egyszerű érték
- csomópont
A csomópont fő típusai
- A dokumentum-csomópontok a teljes dokumentumot reprezentálják
- A
doc(url)parancs hatására jön létre - Minden XPath (és XQuery) lekérdezés hivatkozik egy dokumentum-csomópontra
- Elemcsomópontok: a tagek és a közöttük lévő dokumentumrészlet
- Attribútumok: a nyitó tagekben szerepelnek és ott kapnak értéket
Utak az XML dokumentumban
- Az XPath segítségével az XML dokumentumokat járhatjuk be. Más szóval utakat adhatunk meg.
- Az utak mindig tételek egy listáját választják ki.
Út kifejezések
- Egyszerű formájában az utak perjel és tagek
sorozatából állnak. A kifejezés perjellel kezdődik.
- Példa: /teázók/teázó/ár
- Informális jelentés: a dokumentum csomópontból kiindulva balról-jobbra haladva kövessük a tageket sorra.
- Attribútumok az utakban: @-jel jelöli
Utak, melyek akárhol kezdődhetnek
- Ha az út a dokumentum pontból indul, akkor a //X útkifejezés megtalálja az összes X gyerekelemet a beágyazottság bármely szintjén, és visszaadja abban a sorrendben, ahogy az a dokumentumban megjelenik,
- illetve ha ez a útkifejezés folytatódik: //X/…, akkor bármely olyan részelemből fog indulni, aminek a tagje X.
- Wildcard: *-karakter
Szűrési feltétel
- A tageket feltételek követhetik.
- Ilyenkor csak azok az útkifejezésre illeszkedő utak kerülnek be az eredménybe, melyek a feltételt is kiekégítik.
Tagek atomi értékű törzsének kiválasztása:
- Ehhez a text() függvényt kell használni
- A hivatalos XPath specifikációban [text()] kifejezést kell írni, a text() függvény igazzal tér vissza, ha a tétel atomi érték.
Tengelyek:
- Általánosan: az útkifejezésekben minden egyes lépésnél tengelyekkel (axes) adhatjuk meg a következő lépésnél feldolgozandó pontok listáját.
- A default tengely a child:: – ami az összes gyermekét veszi az aktuális pontoknak.
XQuery
- Az XQuery egy SQL-hez hasonló lekérdezőnyelv, ami XPath kifejezéseket használ.
- Ugyanúgy a tételek listája adatmodellt használja.
- Az XQuery egy funkcionális nyelv.
Tételek listája
- Az XQuery-ben előfordulhat, hogy listák listája generálódik.
- Az ilyen listákat a rendszer "sima" listává alakítja át. (flatten)
FLWR kifejezések
- Egy vagy több
forés/vagyletzáradék. - Ezek után opcionálisan egy
wherezáradék. - Végül egy
returnzáradék.
- Mindegyik
foregy ciklust generál. - a
leta cikluson belüli hozzárendeléseket adja meg. - Minden iterációjánál a beágyazott ciklusnak, ha
van ilyen, ki kell értékelni a
wherezáradékot. - Ha a
wherezáradék IGAZ, areturnzáradéknak megfelelő értéket a végeredményhez kapcsoljuk.
FOR záradék
for <változó> in <kifejezés>, . . .- A változók
$jellel kezdődnek. - A
forváltozója egy ciklusban sorra bejárja a kifejezés eredményének összes tételét. - A
forután megadott részek tehát minden egyes tételre végrehajtódnak egyszer.
LET záradék
let <változó> := <kifejezés>, . . .
- A változó értéke tételek listája lesz, ez a lista a kifejezés eredménye.
- A
letzáradék hatására nem indul el egy ciklus; aforzáradék hatására igen.
Order-By záradék
- Az FLWR valójában FLWOR, ahol egy
order-byzáradék előzheti meg areturnzáradékot. - Alakja:
order by <kifejezés> - A kifejezés a változók minden hozzárendelésére kiértékelődik.
- A végeredmény listájának sorrendjén változtat.
Predikátumok
- A feltételekben a "létezést" követeljük meg.
- Példa: ```/teázók/teázó[@név]`` jelentése "az összes olyan teázó, aminek létezik neve."
- Példa:
/teázók/tea[@árulja = ”JoeTeázója”]azon teázók listáját adja vissza, melyeket Joe teázójában megkaphatunk.
Az elemek adatainak kinyerésére
- Tegyük fel, hogy elemek értékeit szeretnénk összehasonlítani.
- Az $E$ elem értékét a data függvény használatával kaphatjuk meg:
data(E).
Ismétlődések kiszűrése
- Használjuk a distinct-values függvényt, aminek a paramétere: elemek listája.
- Finomság: a függvény a tagek nélkül veszi az értékeket és ezek szöveges értékét hasonlítja össze.
Halmazműveletek
- A union, intersect, except itt is alkalmazhatóak pontok listájára.
- A jelentés hasonló SQL-beli jelentéshez.
- Az ismétlődések itt is törlődnek.
- Az eredmény elemei dokumentum sorrendben jelennek meg.
Összesítések
- Összesítő függvények:
count, sum, max, min, avgitt is megvannak - Ezek bemenete tételek listája
- Ez lehet üres lista is, viszont ennek a kezelésében már eltérő viselkedést mutatnak
Összekapcsolások
- Az XQueryben össze lehet kapcsolni két dokumentumot
- Változók kellenek a megfelelő dokumentumokra
- A for záradék kell egy dokumentum elemeinek előállítására
Források
12. Extra - Analitikus adatfeldolgozás
-
Döntéstámogató rendszerek
- Kevesebb, de kölcségesebb kérések (OLAP kérések)
-
Bitmap indexek
- a dimenziótáblák mindegyik olyan attribútumára, amelyeket várhatóan részt fognak venni egy keresésben. (pl.: minden gyártóra a Tea relációban), eg bitvektor létrehozása, amely megmondja, hogy mey sorok tartalmazzák ezt az értéket
-
Materializált nézetek:
- olyan nézetek, amelyek több lekérdezés megválaszolásához hasznosak magában az adatbázisban eltárolják
Adatbázisok I. gyakorlat
Alapadatok
Idő: Kedd, 16:00 - 18:00
Helyszín: Északi Tömb 7.15 (PC11)
Oktató: Varga Dániel, vargadaniel@inf.elte.hu
Csoport: 10
Értékelés
- Két ZH
- min 40%
- egyet lehet javítani (vagy rontani)
- Folyamatos számonkérés, minden gyakorlaton egy feladat
- 10-ből 7-nek meg kell lennie
- Pluszpontok - ZH-khoz adódik hozzá
Források
1. Gyakorlat
Alap SQL kifelyezések: SELECT, FROM, WHERE, CREATE TABLE.
Források
2. Gyakorlat
Otthonról csak tunel-en keresztül lehet elérni az adatbázisokat.
Több SQL szintaxis elemeket ismertünk meg
LIKEINBETWEENASDISTINCTUNIONINTERSECTMINUSORDER BY
Relációs algebra bevezetés(lsd.:előadás)
Források
- Tunnel instrukciók
- Könyv ide tartozó fejezete
- Gyakorlati feladatok
- RelaX help
- SQL segédanyagok:
3. Gyakorlat
Összekapcsolások SQL-ben és relációs algebrában.
Források
4. Gyakorlat
Relációs algebra feladatmegoldás.
Otthoni plusz pont
Relációs algebrában: Ki az a dolgozó akinek legnagyobb fizetése?
Források
5. Gyakorlat
SQL gyakorlás, új függvények
Források
6. Gyakorlat
Csoportosítás, alkérdés, kiterjesztett relációs algebra
Források
7. Gyakorlat
Alkérdések, DML, DDL
Források
8. Gyakorlat - ZH
9. Gyakorlat
Források
10. Gyakorlat
PL/SQL alapok
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
12. Gyakorlat
Kurzor, PL/SQL kollekciók
Analízis II. (F) előadás
Alapadatok
Idő: Szerda, 8:00 - 10:00
Helyszín: Déli Tömb 0-803 Szabó József előadó
Oktató: Szili László
Csoport: 1
Értékelés
- Írásbeli vizsga
- 15 kérdés: definíciók / tételek
- min 8 pont
- 2 tétel megfogalmazása és bizonyítása
- legalább az egyik kimondása és bizonyítása megfelelő.
- Ha megvan a 2-es, szóban lehet javítani
- 15 kérdés: definíciók / tételek
Források
Differenciálszámítás I.
Emlékeztető a függvény határértékről

Most a legfontosabb határérték végesben vett véges határérték lesz.
Határértéket torlódási pontban értelmezünk.
Derivált
Motiváció
- Függvények töréspontjának elemzése
- Szelő meredeksége:
- Ha , akkor a fügvvény deriválható pontban.
- Pillanatnyi sebesség
Belső pont
Tegyük fel, hogy Az pont az halmaz belső pontja, ha
Az sziombólummal jelöljük az halmaz belső pontjainak halmazát.
Derivált definíciója
Az függvény az pontban differenciálható, ha létezik és véges a határérték.
Ezt a határértéket nevezzük az függvény pontbeli deriváltjának. ()
Ennek létezésének tényét következőképp fogjuk jelölni:
A folytonosság és a deriválhatóság kapcsolata
Tegyük fel, hogy és ekkor:
- Az állítás fordítva nem igaz.
Az érintő fogalma
Az függvény grafikonjának az pontban van érintője, ha . Az függvény grafikonjának pontbeli érintőjén az egyenletű egyenest értjük.
Deriválási szabályok
- , ha
- , ha
Inverz függvény deriváltja
Legyen egy nyílt intervallum, és . Tegyük fel, hogy:
- szigorúan monoton és folytonos az intervvalumon,
- valamilyen pontban és
Ekkor az függvény deriválható a pontban, és
Hatványsor összegfüggvényének deriváltja
Legyen és . Tegyük fel, hogy hatványsor konvergenciasugara pozitív, és jelölje az összegfüggvényt: Ekkor minden pontban és
Derivált függvény
Ha és , akkor az
függvényt az deriváltfüggvénynek nevezzük, és az szimbolummal jelöljük.
Források
Differenciálszámítás II. és függvénytulajdonságok kapcsolata a deriválttal I.
- Differenciálszámítás II. és függvénytulajdonságok kapcsolata a deriválttal I.
Egyoldali pontbeli deriváltak
Vannak olyan esetek, amikor a differenciálhányados létezését a bal és a jobb oldali határértékek egyezésével szükséges vizsgálni.
Legyen és olyan pont, hogy . Azt mondjuk, hogy az függvény jobbról deriválható az pontban, ha létezik és véges a határérték.
Ezt a határértéket az szimbólummal jelöljük, és az függvény jobb oldali deriváltjának nevezzük.
A bal oldali deriváltat pontban hasonlóképp értelmezzük.
Magasabb rendű deriváltak
Egy függvényt többször is deriválhatunk (rekurzió).
Legyen és . Azt mondjuk, hogy kétszer deriválható az pontban, ha
- , és
- az deriváltfüggvény deriválható -ban, azaz
Legyen ekkor az függvény -beli második deriváltja.
Legyen és , és tegyük fel, hogy valamely esetén létezik az -gyel jelölt -edik deriváltfüggvény. Azt mondjuk, hogy -szer deriválható az pontban (jelölése: ), ha
- , és
- az deriváltfüggvény deriválható -ban, azaz
Legyen ekkor az függvény -beli -edik deriváltja.
Leibniz-szabály
Ha valamilyen esetén , akkor
- és
- és
Lokális szélsőértékek
Az függvénynek az pontban lokális maximuma van, ha
Ekkor az pontot lokális maximumhelyének nevezzük, az függvény-érték pedig a függvény lokális maximuma.
A lokális minimumot hasonlóképp definiálhatjuk.
A lokális szélsőértékre vonatkozó elsőrendű szükséges feltétel
Tegyük fel, hogy és
- valamilyen -ben
- -nek -ban lokális szélsőértéke van
Ekkor
Az függvénynek az stacionárius pontja, ha és
A differenciálszámítás középértéktételei
Rolle-féle középértéktétel
Legyen és . Ekkor
Cauchy-féle középértéktétel
Legyen és . Ekkor
Lagrange-féle középértéktétel
A Rolle-féle középértéktétel ezen tétel speciális esete.
Legyen és . Ekkor
Deriváltak egyenlősége
Legyen és .
- Tegyük fel, hogy és . Ekkor
- Tegyük fel, hogy és . Ekkor
Monotonitás
Az egyszerűség kedvéért csak intervallumon vizsgáljuk.
Az első derivált előjeléből következtethetünk a monotonitásra.
A monotonitás és a derivált kapcsolata
Legyen egy nyílt intervallum. Tegyük fel, hogy . Ekkor
A lokális szélsőértékre vonatkozó elégséges feltételek
A lokális szélsőértékre vonatkozó elsőrendű elégséges tétel
Legyen és . Tegyük fel, hogy
- egy pontban
- az deriváltfüggvény előjelet vált -ben.
Ekkor:
- Ha az függvény a pontban negatív értékből pozitív értékbe megy át, akkor az függvénynek lokális minimumhelye.
- Ha az düggvény a pontban pozitív értékből negatív értékbe megy át, akkor az függvénynek lokális maximumhelye.
A lokális szélsőértékre vonatkozó másodrendű elégséges tétel
Legyen és . Tegyük fel, hogy
- kétszer deriválható egy pontban, azaz
Ekkor lokális szélsőértékhelye az függvénynek:
- Ha , akkor -nek -ben lokális minimuma van
- Ha , akkor -nek -ben lokális maximuma van
Források
Függvénytulajdonságok kapcsolata a deriváltal II.
Konvex és konkáv függvények
Legyen és egy intervallum. Ha esetén igaz az, hogy
- ha , akkor azt modnjuk, hogy az függvény konvex az intervallumon.
- ha , akkor azt modnjuk, hogy az függvény konkáv az intervallumon.
Szigorú egyenlőtlenségek esetén szigorúan konvex/konkáv függvényekről beszélünk.
A konvexitás-konkávitás és a második derivált kapcsolata
Legyen egy nyílt intervallum. Tegyük fel, hogy . Ekkor
- konvex [illetve konkáv] -n [illetve ] -n
- ha [illetve ] -n szigorúan konvex [illetve sziorúan konkáv] -n
Inflexiós pont
Legyen egy nyílt intervallum és tegyük fel, hogy . Ekkor azt mondjuk, hogy a pont az függvény inflexiós pontja, ha vagy fordítva.
Aszimptoták
Legyen és . Azt mondjuk, hogy az függvénynek van aszimptotikája ()-ben, ha elsőfokú függvény, amelyre
Ekkor az egyenletű egyenes az függvény asszimptotikája ()-ben.
Tétel
Legyen . Az függvénynek akkor és csak akkor van asszimptotikája ()-ben, ha léteznek és vegesek a következő határértékek:
Ekkor az egyenes az függvény asszimptotikája ()-ben.
L'Hospital szabályok
0/0 esetben
Legyen , illetve . Ekkor
- és
Végtelen/Végtelen esetben
Legyen , illetve . Ekkor
- és
Teljes függvényvizsgálat
- Kezdeti vizsgálatok (Deriválhatóság, zérushelyek, előjelvizsgálat, paritás, periodicitás megállapítása)
- Lokális szélsőértékek ls monotonitási intervallumok
- Konvexitási intervallumok és inflexiós pontok
- Határértékek és aszimptoták
- A függvény grafikonjának felrajzolása
Források
Speciális függvények
- Speciális függvények
Már elemzett speciális függvények
Analízis I tárgyból, már vizsgáltunk pár speciális függvényt, de a konvexitásukra a deriválás ismeretének hiányában nem tudtunk kitérni.
Exponenciális függvény
Az függvény szigorúan konvex -en, ha és . Ez abból következik, hogy minden esetén
Ha , akkor az lineáris függvény egyszerre konvex és konkáv -n, de nem szigorú értelemben.
Logaritmus függvény
A függvény szigorúan konkáv -n, ha , és szigorúan konvex -n, ha , hiszen minden esetén
- , ha
- , ha
Mivel , ha , illetve , ha .
Hatványfüggvény
Az függvény konvexitása is függ az értékétől.
Minden esetén
(x^{\alpa})^{\prime\prime} = (\alpha x^{\alpha - 1})^{\prime} = \alpha(\alpha - 1)x^{\alpha - 2}
Tehát az előjelén múlik a függvény konvexitása.
Ha vagy , akkor , és így az függvény konvex -n.
Ha , akkor , és így az függvény konkáv -n.
Ha vagy , akkor lineáris függvény, azaz egyszerre konvex és konkáv -n, de nem szigorú értelemben.
Trigonometrikus függvények
A sin és cos függvény
-
Paritás: a függvény páratlan, és a függvény páros, azaz
-
Addíciós képletek: minden esetén:
- Két szinusz és koszinusz összege szorzattá alakítható
- (lsd.: jegyzet)
-
Minden esetén:
-
Négyzetes összefüggés:
-
Folytonosság: A és a függvény folytonos -en.
-
szám értelmezése: legyen a függvény egyetlen zérushelye a intervallumon.
-
Az addíciós tételből a következő kapcsolat adódik:
-
Periodicitás: A és a függvény szerint periodikus.
-
Differenciálhatóság: A és a függvény differenciálható -en és
Szinusz és koszinusz monotonitásáról és konvexitásáról szóló tétel
- -en, -n és szigorúan konkáv -n
- -n, szigorúan konkáv -en és szigorúan konvex -n
A szinusz függvény
- -en, -en és -n
- szigorúan konvex -n
- inflexiós pont.
A koszinusz függvény
-
-n és -n
-
szigorúan konvex -en
-
szigorúan konkáv -en
-
szigorúan konvex -n
-
inflexiós pontok
A tangens és kotangens függvény
- páratlan függvény, azaz
- a függvény szerint periodikus
- a függvény zérushelyei:
- -en
- szigorúan konkáv -en
- szigorúan konvex -en
- inflexiós pont
- és
- páratlan
- szerint periodikus
- \arrowdown (0, \pi)-n
- szigorúan konvex -n
- szigorúan konkáv -n
- infleciós pont
- és
Trigonometrikus függvények inverzei
- folytonos -en
- deriválható -en és
- -en
- szigorúan konkáv -en
- szigorúan konvex -en
- inflexiós pont
- folytonos -en
- deriválható -en és
- -en
- szigorúan konvex -en
- szigorúan konkáv -en
- inflexiós pont
- folytonos és deriválható -en és
- -en
- szigorúan konvex -n
- szigorúan konkáv -en
- inflexiós pont
- aszimptota a -ben
- folytonos és deriválható -en és
- -en
- szigorúan konkáv -n
- szigorúan konvex -en
- inflexiós pont
- aszimptota a -ben
- aszimptota a -ben
Hiperbolikus függvények
- páratlan függvény
- folytonos és deriválható -en és
- -en
- szigorúan konkáv -n
- szigorúan konvex -en
- inflexiós pont
- páros függvény
- folytonos és deriválható -en és
- -en és -en
- szigorúan konvex -n
- abszolút minimumhely
- páratlan függvény
- folytonos és deriválható -en és
- -en
- szigorúan konvex -n
- szigorúan konkáv -en
- inflexiós pont
- aszimptota -ben
- páratlan függvény
- folytonos és deriválható -en és
- -en és -n
- szigorúan konkáv -n
- szigorúan konvex -en
- aszimptota -ben
Hiperbolikus függvények inverzei
Tétel
Források
Taylor polinomok és Taylor sorok
Lineáris közelítés
Gyakori jelenség, hogy valamely problémánál fellépő függvénnyel dolgozva egyszerűbb és áttekinthetőbb eredményhez juthatunk, ha a függvény helyett egy másik, az eredetit "jól közelítő", de egyszerűbb típusú függvényt tekintünk. Az egyik legegyszerűbb függvénytípus az elsőfokú polinom (vagyis az függvény). Megmutatjuk, hogy egy függvény deriválhatósága az pontban éppen azt jelenti, hogy a függvény bizonyos értelemben "jól közelíthető" elsőfokú polinommal.
Legyen és . Ekkkor
Taylor polinomok
Ha a lineáris közelítés nem elég pontos, akkor magasabb fokszámú polinomokkal is próbál- kozhatunk. Jobbnak tűnik az típusú közelítés, ahol és egy legfeljebb -ed fokú polinom.
A továbbiakban feltételezzük, hogy és az függvény -szer deriválható az pontban. Ekkor értelmezhető az alábbi polinom.
Ha és , akkor a polinomot az függvény ponthoz tartozó -edik Taylor-polinómjának nevezzük.
A Taylor polinom úgy van kitalálva, hogy -dik deriváltja megegyezik a függvénx -fik deriváltjával az pontban.
Taylor formula
A Taylor-polinommal történő közelítés becsléséhez szükségünk lesz a következő állításra.
Legyen és tegyük fel, hogy Ekkor a fenti képlet jobb oldalán álló függvényt Lagrange-féle maradéktagnak nevezzük.
Taylor sorok
Egy adott függvényt vajon elő lehet-e állítani hatványsor összegfüggvényeként? Ha igen, akkor a függvény ismeretében hogyan lehet az együtthatókat meghatározni?
Ha és , akkor a hatványsort az függvény ponthoz tartozó Taylor sorának nevezzük.
Minden pozitív konvergenciasugárral rendelkező hatványsor összefüggvénye a Taylor sorával egyenlő a konvergenciahalmaz belsejében.
Elégséges feltétel függvények Taylor sorral történő előállítására
Legyen , és tegyük fel, hogy valós szám, amire teljesül. Ekkor -nek az ponthoz tartozó Taylor sora a halmazon előállítja az függvényt, vagyis fennáll a következő egyenlőség:
Források
Integrálszámítás I
A határozatlan integrál fogalma
Legyen adott nyílt intervallumon értelmezett függvény.
Azt mondjuk, hogy a függvény primitív függvénye, ha és
Tétel
Legyen nyílt intervallum és adott függvény.
- Ha az függvénynek egy primitív függvénye, akkor minden esetén a függvény is primitív függvénye -nek
- Ha primitív függvényei az függvénynek, akkor azaz a primitív függvények csak konstansban különböznek egymástól.
Ennél a tételnél fontos, hogy intervallumon legyen értelmezve!
Az nyílt intervallumon értelmezett függvény primitív függvényeinek a halmazát határozatlan integráljának nevezzük, és így jelöljük: Ilyenkor -re az integrandus, illetve az integráló függvény elnevezéseket használjuk.
Határozatlan integrálra vonatkozó szabályok
A határozatlan integrál linearitása
Legyen nyílt intervallum.
Ha az függvényeknek létezik primitív függvénye, akkor tetszőleges
mellett -nek is létezik primitív függvénye és
Az első helyettesítési szabály
Legyenek nyílt intervallumok és függvények.
Tegyük fel, hogy és az függvénynek van
primitív függvénye. Ekkor az függvénynek is van
primitív függvénye és
Parciális integrálás
Legyen nyílt intervallum. Tegyük fel, hogy és az függvénynek létezik primitív függvénye -n. Ekkor az függvénynek is van primitív függvénye ls
A második helyettesítési szabály
Legyenek nyílt intervallumok.
Tegyük fel, hogy -n
és az függvénynek van primitív függvénye.
Ekkor az függvénynek is van primitív függvénye és
Források
Integrálszámítás II
- Integrálszámítás II
Határozott integrál
Tegyük fel, hogy és egy korlátos függvény. Azt mondjuk, hogy Riemann-integrálható az intervallumon, ha Ekkor az számot az függvény intervallumon vett Rienmann-integrálnak nevezzük. Az intervallumon Riemann-integrálható függvények halmazát az szimbólummal fogjuk jelölni.
Ha a korlátos függvény Riemann-integrálható az intervallumon és , akkor az grafikonja alatti síkidomnak van területe, és a területét így értelmezzük:
A határozott integrál tulajdonságai
-
Legyen és tegyük fel, hogy az halmaz véges. Ekkor
- ha , akkor
-
Legyen . Tegyük fel, hogy az függvény folytonos.
Ekkor , azaz minden folytonos függvény integrálható () -
Legyen . Ha az függvény szakaszonként folytonos, akkor és
-
Tegyük fel, hogy . Ekkor
-
minden esetén
-
-
ha valamilyen állandóra fennáll az egyenlőtlenség, akkor függvény is integrálható az intervallumon.
-
-
Tegyük fel, hogy . Ekkor
- ha és , akkor
- , és
Intervallum szerinti additivitás
Legyen valós számok és korlátos függvény. Ekkor akkor és csak akkor, ha Ekkor
Az integrálfüggvény
Tegyük fel, hogy és . Az függvény az függvény pontban eltűnő integrálfüggvénynek nevezzük.
Az integrálfüggvény folytonossága
Legyen és a függvény pontban eltűnő integrálfüggvénye. Ekkor
Az integrálfüggvény deriválhatósága
Legyen és az függvény pontban eltűnő integrálfüggvénye.
Tegyük fel, hogy olyan pont, amire teljesül.
Ekkor és
A határozott integrál kiszámítása
Legyen korlátos és zárt intervallum. A függvény az függvény egy primitív függvénye az intervallumon, ha
- és
Newton Leibniz formula
Tegyük fel, hogy
- és
- az függvénynek van primitív függvénye az intervallumon Ekkor ahol az függvény egy primitív függvénye.
A határozott integrál alkalmazása
Ívhossz
Legyen és adott függvény. Azt mondjuk, hogy a függvénygrafikon rektifikálható (van ívhossza), ha Ezt a valós számot a szóban forgó függvénygrafikon ívhosszának nevezzük.
Legyen és tegyük fel, hogy Ekkor az függvény grafikonjának van ívhossza, és az egyenlő az határozott integrállal.
Forgástest térfogata
Legyen . Ekkor grafikonjának az tengely körüli megforgításával adódó forgástestnek van térfogata, és az egyenlő a integrállal.
Legyen és tegyük fel, hogy . Ekkor grafikonjának az -tengely körüli forgatásával adódó forgásfelületnek van felszíne, és értéke
Improprius integrálok
Legyen és . Tegyük fel, hogy minden esetén. Vezessük be a függvényt. Azt mondjuk, hogy függvény impropriusan integrálható, ha véges határérték. Ekkor az számot az improprius integráljának nevezzük.
Legyen és . Tegyük fel, hogy minden esetén. Azt mondjuk, hogy az függvény impropriusan integrálhatóm ha minden esetén és impropriusan integrálható. Ekkor legyen
Források
Többváltozós függvénytan I
Konvergencia az euklideszi térben
Az függvényt -beli sorozatnak nevezzük. Az helyettesítési érték a sorozat k-adik vagy k-indexű tagja. A tag sorszámát jelző szám a tag indexe.
Legyen . Azt mondjuk, hogy az euklideszi tér sorozata konvergens, ha Ha létezik, akkor az egyértelmű, és -t az sorozat határértékének nevezzük. Az sorozat divergens, ha nem konvergens.
Tétel
Legyen . Egy -beli sorozat akkor és csak akkor konvergens, ha a sorozat minden koordinátasorozata konvergens, és a határértéke a határvektor megfelelő koordinátája, azaz pontosan akkor ogaz, ha minden koordinátára
Cauchy féle konvergenciakritérium
Legyen Az euklideszi tér sorozata akkor és csak akkor konvergens, ha Cauchy-sorozat, azaz
Bolzano-Weierstrass kiválasztási tétel
Az euklideszi térben minden korlátos sorozatnak van konvergens részsorozata.
típusú függvények folytonossága
Azt mondjuk, hogy az függvény folytonos az pontban, ha
Folytonosságra vonatkozó átviteli elv
Legyen és . Ekkor
Tétel
Legyen és a \in \mathxal{D}_f. Ekkor ahol az függvény koordinátafüggvényei.
Weierstrass tétele
Legyen és tegyük fel, hogy
- korlátos és zárt halmaz az euklideszi térben
- Ekkor az függvénynek vannak abszolút szélsőértékhelyei, azaz \eixsts x_1 \in \mathcal{D}_f, \ \forall x \in \mathcal{D}_f : f(x) \leq f(x_1) \eixsts x_2 \in \mathcal{D}_f, \ \forall x \in \mathcal{D}_f : f(x_2) \leq f(x)
típusú függvények határértéke
Az függvények az pontban van határértéke, ha , hogy Ekkor -t a függvény pontbeli határértékének nevezzük.
A határértékre vonatkozó átviteli elv
Legyen és a \in \matcal{D}_f^{\prime}. Ekkor
Tétel
Tegyük fel, hogy és Ekkor
Források
9. Többváltozós függvények deriválása I
- 9. Többváltozós függvények deriválása I
Parciális deriváltak typusú függvényekre
Tegyük fel, hogy f \in \R^n \to \R (n \in \N^+), \ a \in \ int\mathcal{D}_f és a kanonikus bázis -ben. Az függvénynek az -ban létezik az -dik változó szerinti parciális deriváltja, ha az valós-valós függvény deriválható a pontban. A valós számot az függvény pontbeli, -edik változó szerinti parciális deriváltjának nevezzük, és az alábbi szimbólumok valamelyikével jelöljük:
Iránymenti deriváltak típusú függvényekre
Legyen és . Tegyük fel, hogy egy egységvektor: . A függvénynek az pontban létezik a irányú iránymenti deriváltja, ha a valós-valós függvény deriválható a pontban. A valós számot az függvény pontbeli irányú iránymenti deriváltjának nevezzük, és a vagy a szimbólumokkal jelöljük.
Tétel
Tegyük fel, hogy , illetve az függvénynek léteznek a parciális deriváltjai egy környezetben, és ezek folytonosak az pontban. Ekkor az függvénynek az pontból induló tetszőleges egységvektor irányban létezik az iránymenti deriváltja, és ahol az úgynevezett gradiensvektor és egységvektor, azaz
A totális derivált típusú függvényekre
Az függvény totálisan deriválható az pontban, ha Ekkor az függvény deriváltmátrixa az pontban.
Tétel I
Tegyük fel, hogy és . Ekkor az deriváltmátrix egyértelműen meghatározott.
Tétel II
Tegyük fel, hogy és . Ekkor
Tétel III
Legyenek az függvények koordinátafüggvényei , ahol , illetve . Ekkor Továbbá , azaz az mátrix -edik sora.
A deriváltmátrix előállítása
Legyen , ahol az függvény -edik koordinátafüggvénye. Ha , akkor a Jacobi-mátrix
Elégséges feltétel a totális deriválhatóságra
Legyen és . Tegyük fel, hogy az pontnak létezik olyan környezete, amelyre minden index esetén a következők teljesülnek:
- minden pontban
- a parciális deriváltfüggvény folytonos az pontban.
Ekkor az függvény totálisan deriválható az pontban.
A totálisan derivált és az iránymenti derivált kapcsolata
Tegyük fel, hogy és . Ekkor minden irányban vett iránymenti deriváltja létezik az pontban, és az úgynevezett gradiensvektor és egységvektor,azaz
Felület érintősíkja
Az függvény grafikonjának az pontban van érintősíkja, ha . Az érintősík egyenlete: amelynek egyik normálvektora:
Deriválási szabályok
Algebrai műveletekre vonatkozó deriválási szabályok
- Ha és f,g \in \D{a}, akkor esetén
- Ha , akkor az és az függvényekre az egyváltozós esethez hasonló deriválási szabályok teljesülnek.
Az összetett függvény deriválhatósága, láncszabály
Legyen . Ha és , továbbá és , akkor és
Források
Többváltozós függvények deriválása II
A gradiens vektor
Legyen és . Ekkor vektort gradiens vektornak nevezzük.
Magasabb rendű deriváltak
Az függvény kétszer deriválható az pontban, ha
- , hogy minden pontban és
- indexre
Ha az függvény kétszer deriválható az pontban, akkor az függvény pontbeli Hesse-féle mátrixa, ahol
Young tétel
Ha és , akkor
A Taylor-formula a Peano-féle maradéktaggal
Legyen és tegyük fel, hogy és . Ekkor van olyan feltételnek eleget tevő függvény, hogy
típusú függvények szélsőértékei
Azt mondjuk, hogy az függvénynek az ponban abszolút maximuma van, ha Ekkor az függvényértéket az abszolút maximumának nevezzük.
Azt mondjuk, hogy az függvénynek az pontban lokális maximumhelye van, ha van olyan környezet, hogy Ekkor az függvényértéket az függvény lokális maximumának nevezzük.
Elsőrendű szükséges feltétel a lokális szélsőértékre
Tegyük fel, hogy és Továbbá
- és
- az függvénynek az pontban lokális szélsőértéke ban Ekkor , azaz
Az pont az függvény stacionárius pontja, ha és
Másodrendű elégséges feltétel a lokális szélsőértékekre
Legyen és egy szimmetrikus mátrix. Ekkor a függvény az mátrix által meghatározott kvadratiks alaknak nevezzük.
Azt mondjuk, hogy az szimmetrikus mátrix, illetve a hozzá tartozó kvadratikus alak
- pozitív definit, ha esetén
- negatív definit, ha esetén
Tétel
Legyen és . Tegyük fel, hogy
- az Hesse-féle mátrix pozitív (negatív) definit. Ekkor az függvénynek az pontban lokális minimuma (maximuma) van.
Másodrendű szükséges feltétel a lokális szélsőértékre
Azt mondjuk, hogy az szimmetrikus mátrix, illetve a hozzá tartozó kvadratikus alak
- pozitív szemidefinit, ha esetén ,
- negativ szemidefinit, ha esetén ,
- indefinit, ha pozitív ls negatív értéket is felvesz
Tétel
Legyen és . Ha az függvénynek az pontban lokális minimuma (maximuma) van, akkor
- az Hesse-féle mátrix pozitív (negatív) szemidefinit.
Sylvester-kritérium
Legyen n \in \N^+, \ A \in \R^{n \times \n} egy szimmetrikus mátrix és az által meghatározott kvadratikus alak. Jelölje az mátrix "bal felső sarokmátrixainak" a determinánsa. Ekkor az mátrix, illetve a kvadratikus alak
- pozitív definit ha esetén
- negatív definit ha esetén
Abszolút szélsőértékek
Legyen korlátos és zárt halmaz. Tegyük fel, hogy az függvény folytonos, illetve deriválható minden belső pontjában. Ekkor a legnagyobb (legkisebb) értékét vagy a halmaz határán veszi fel, vagy pedig egy olyan belső pontban, ahol teljesül minden indexre.
Források
Többváltozós függvények deriválása III
- Többváltozós függvények deriválása III
Az inverzfüggvény-tétel
Legyen nyílt halmaz és . Tegyük fel, hogy
- folytonosan deriválható -n
- az pontban
Ekkor
- lokálisan invertálható az pontban, azaz vannak olyan és nyílt halmazok, hogy az függvény bijekció (következésképpen invertálható)
- az inverz függvény folyamatosan deriválható -n és
Implicit függvények
Egyváltozós implicitfüggvény-tétel
Legyen nyílt halmaz és . Tegyül fel, hogy
- folyamatosan deriválható -n
- az pontban és
Ekkor
- van olyan környezet és nyílt halmaz -ben, hogy minden ponthoz létezik egyetlen , amelyre f(x, \varhi(x)) = 0 teljesül
- az így definiált függvény folytonosan deriválható -n és
Implicitfüggvény-tétel az általános esetben
Legyenek és nyílt halmazok , illetve . Tegyük fel, hogy
- folytonosan deriválható az halmazon
- az pontban és
Ekkor
- létezik -nak olyan környezet és nyílt halmaz, hogy minden ponthoz létezik egyetlen , amelyre
- az így definiált függvény folytonosan deriválhatü -n és
típusú függvények feltételes szélsőértékei
Legyen nyílt halmaz. Tegyük fel, hogy adott függvények és
Azt mondjuk, hogy az függvénynek a feltétel mellett az pontban
- feltételes abszolút maximuma van, ha
- feltételes lokális maximuma van, ha
Szükséges feltétel a feltételes lokális szélsőértékre
Tegyük fel, hogy
- nyílt halmaz és az függvényeknek léteznek a parciális deriváltjaik, és ezek folytonosak az halmazon (f,g \in \C^1(U))
- az pontban az függvénynek a feltételre vonatkozóan feltételes lokális szélsőértéke van.
- Ekkor can olyan valós szám (Lagrange-szorzó), hogy az Lagrange-függvénynek stacionárius pontja, azaz
Feltételes lokális szélsőértékre vonatkozó másodrendű elégséges feltétel
Tegyük fel, hogy
- nyílt halmaz és az függvényeknek léteznek másodrendű parciális deriváltjaik és ezek folytonosak az halmazon.
- az pontban a számmal teljesül a szükséges feltétel.
Tekintsül ezzel a \lamba_0 számmal az Lagrange-függvényt. Legyen
Ekkor
- feltételes lokális maximumhely
- feltételes lokális minimumhely
Források
Analízis II. (F) gyakorlat
Alapadatok
Idő: Hétfő, 10:00 - 12:00
Helyszín: Északi Tömb -1.62
Oktató: György Szilvia
Csoport: 1
Értékelés
- 10 kisZH (definíció, tétel előadásból és órai/házi feladat)
- max 40 pont
- min 16
- 2 ZH (ápr 6-7 és máj 25-26)
- max 40 - 40 pont
- min 11 pont
- Megajánlott vizsgajegy:
- ZH-kon tételek (min 5p)
- Gyak jegy
- kisZH 12p tételekre, definíciókra
Források
1. Gyakorlat
Deriválás definíciójával ekvivalens határérték
Derivációs feladatok
- Deriválható-e egy adott függvény adott pontban?
- Ha a függvény definíciója miatt adott pontban két határértéket kell vizsgálni, akkor csak akkor deriválható, ha jobbról és balról is van határértéke adott pontban, és ezek a határértékek megegyeznek.
- Deriválás deriválási szabályokkal
- Összetett függvények deriválása
Deriválási szabályok
- , ha
Ajánlott házi feladatok
Feladatsor órai részéből:
-
- c,d
-
- c
-
- b,d
-
- c,d
Források
2. Gyakorlat
Feladatok
- Egyenes érintője pontban.
- Inverz függvény deriváltja pontban.
- Inverz függvény deriváltfüggvénye.
- Egyoldali pontbeli deriváltak.
Ajánlott házi feladatok
Feladatsor órai részéből:
-
- b
-
- c,d
-
- b
-
-
(a 6,7. feladatok nem ZH típusfeladatok)
Források
3. Gyakoralt
Feladatok
- Monotonitási intervallumok megadása
- Lokális szélsőértékek és szélsőértékhelyek
- Abszolút szélsőértékek és szélsőértékhelyek
Ajánlott házi feladatok
-
- kiszámítása
-
-
Források
4. Gyakorlat
Feladatok
- L'Hospital szabályok alkalmazása
- Már tört alakban lévő függvények határértékeihez
- Olyan függvényekre, melyeket tört formára kell előbb hozni
- alakú függvények esetében
- Konvex / konkáv intervallumok megadása és inflexiós pont
Új deriválási szabály
Ajánlott házi feladatok
-
- c, d: átalakítás nélkül, rögtön L'Hospotal szabállyal
-
- a, c
Források
5. Gyakorlat
Feladatok
- Aszimptoták számítása
- Teljes függvényvizsgálat
- monotonitás
- lokális/abszolút szélsőértékek
- konvexitás, inflexiós pont
- határértékek, aszimptoták
- ábrázolás
- Elemi függvények
Ajánlott házi feladadtok
- Feladatsorokban látott deriválások elvégzése
Források
6. Gyakorlat
Feladatok
- Lineáris közelítés
- Taylor polinom
- Taylor polinom hibabecslése
Ajánlott házi feladatok
-
- a: hibabecslés, c: -ra hibabecslés
-
-
-
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
8. Gyakorlat
Feladatok
- Határozatlan integrál számítás
- Határozatlan integrál számítás speciális esetekben
Ajénllott házi feladatok
- (2 módszerrel)
Források
9. Gyakorlat
Feladatok
- Határozatlan integrálok parciális integrálással
- típus
- típus
- típus
- Racionális törtek integrálása
Ajánlott házi feladatok
- fs1 / 3) a
- fs1 / 4) b
- fs1 / 6) a, b
Források
10. Gyakorlat - elmaradt, pótlás várható
11. Gyakorlat
Feladatok
- Parciális deriválás
- Másodrendű parciális deriválás
- Iránymenti deriválás
- Totális deriválás
Ajánlott házi feladatok
- Egyszerűsítés gyakorlás
- Kihagyott feladatok
Források
12. Gyakorlat - nincs jegyzet
Tételbizonyítások
Bizonyítással kért tételek I.
- A folytonosság és a deriválhatóság kapcsolata
- A szorzatfüggvény deriválási szabálya
- A hányadosfüggvény deriválási szabálya
- Az inverz függvény deriválási szabálya
- A lokális szélsőértékre vonatkozó elsőrendű szükséges feltétel
- A Rolle-féle középértéktétel
- A Cauchy-féle középértéktétel
- A monotonitás és a derivált kapcsolata
- A konvexitás és a kétszeres derivált kapcsolata
- A L'Hospital-szabály a 0/0 esetben
- A deriválhatóság ekvivalens átfogalmazása lineáris közelítéssel
- A Taylor-formula a Lagrange-féle maradéktaggal
- Elégséges feltétel függvények Taylor-sorral történő előállítása
Bizonyítással kért tételek II.
- A határozatlan integrál linearitása
- A parciális integrálás szabálya
- A második helyettesítési szabály
- Az integrálfüggvény folytonossága
- Az integrálfüggvény deriválhatósága
- A Newton-Leibniz-formula
- Egy vektorsorozat és koordinátasorozatai konvergenciájának kapcsolata
- A deriváltmátrix egyértelműsége
- A deriváltmátrix előállítása
- A totális- és az iránymenti derivált kapcsolata
- típusú függvényekre vonatkozó elsőrendű szükséges feltétel a lokális szélsőértékre
- típusú függvényekre vonatkozó másodrensű elégséges feltétel a lokális szélsőértékre
- típusú függvényekre vonatkozó másodrendű szükséges feltétel a lokális szélsőértékre
Források
A folytonosság és a deriválhatóság kapcsolata
Kimondás
Tegyük fel, hogy és Ekkor
- ,
- Az állítás megfordítása nem igaz.
Bizonyítás
-
Ha , akkor ez éppen azt jelenti, hogy .
-
Van olyan folytonos függvény, amelyik egy pontban folytonos, de ott nem deriválható.
Például az abszolút érték függvény az pontban.
Valóban , de , hiszen minden esetén ami , ha és , ha és így Ezért az függvény pontbeli differenciálhányadosa nem létezik.
A szorzatfüggvény deriválási szabálya
Kimondás
Tegyük fel, hogy és valamilyen pontban.
Ekkor
Bizonyítás
Nyilván , hiszen . Másrészt
A hányadosfüggvény deriválási szabálya
Kimondás
Tegyük fel, hogy és valamilyen pontban.
és
Ekkor
Bizonyítás
. Ha , akkor , ezért a feltétel miatt , hiszen a folytonos függvények előjeltartóak. Mivel , így feltételezhetjük, hogy sugara olyan kicsi, hogy a fentiek mellett is teljesül. Ekkor , és így Másrészt
Az inverz függvény deriválási szabálya
Kimondás
Legyen egy nyílt intervallum, és .
Tegyük fel, hogy
- szigorúan monoton és folytonos az intervallumon,
- valamilyen pontban és .
Ekkor az függvény deriválható a pontban és
Bizonyítás
Tufjuk, hogy ha szigorúan monoton, akkor invertálható és inverze is szigorúan monoton. Mivel egy nyílt intervallum, illetve szigorúan monoton és folytonos függvény, így is egy nyílt intervallum, ezért , illetve folytonos ennek az nyílt intervallum minden pontjában.
Legyen . Tudjuk, hogy és . Mivel szigorúan monoton, így egyértelmű, ezért alkalmazhatjuk az helyettesítést az alábbi határértékben, ahol , ha és ( folytonossága miatt).
hiszen és
A lokális szélsőértékre vonatkozó elsőrendű szükséges feltétel
Kimondás
Tegyük fel, hogy és
- valamilyen -ben,
- -nek -ban lokális szélsőértéke van.
Ekkor
Bizonyítás
Tegyük fel, hogy az pont lokális maximumhelye az függvénynek. Ekkor
Tekintsünk az függvény -hoz tartozó különbséghányados-függvényét:
Ha , azaz , akkor (vagyis ) miatt -ben szereplő különbséghányados nem pozitív. Mivel , ezért
Ha , azaz , akkor (vagyis ) miatt -ben szereplő különbséghányados nem negatív. Mivel , ezért
Azt kaptuk tehát, hogy és , ami csak úgy lehetséges, ha .
A bizonyítás hasonló akkor is, ha az pont lokális minimumhelye as függvénynek.
A Rolle-féle középértéktétel
Kimondás
Legyen és . Ekkor
Bizonyítás
Mivel , ezért a Weierstrass tételből következik, hogy
Két eset lehetséges
- Ekkor állandó -n, így tetszőleges pontban .
- , tehát
Ha , akkot az abszolút minimumhely az intervallumban van. Világos, hogy egyúttal lokális minimumhelye is az függvénynek. A feltételeink alapján , ezért a lokális szélsőértékre vonatkozó elsőrendű szükséges feltételből következik, hogy . A tétel állítása tehát a választással teljesül.
Ha , akkor a abszolút maximumhely van az intervallumban, és ez egyúttal lokális maximumhely is, tehát . Ebben az esetben a tétel állítása tehát a választással teljesül.
A Cauchy-féle középértéktétel
Kimondás
Legyen és . Ekkor
- ,
- ,
Bizonyítás
Először vegyük észre, hogy a Rolle-tételből következik, hogy .
Tekintsük a következő függvényt:
Világos, hogy
Másrészt
Ez azt jelenti, hogy eleget tesz a Rolle-tétel feltételeinek, és így
Azonban tehát
A monotonitás és a derivált kapcsolata
Kimondás
Legyen egy nyílt intervallum. Tegyük fel, hogy . Ekkor
Bizonyítás
- Ha -n és egy tetszőleges pont, akkor
hiszen és a monotonitás miatt . Mivel , így
Ha , akkor legyen két tetszőleges pont.
Ekkor , és így a Langrange-féle középértéktétel szerint
Ezért -n.
Az állítás hasonlóan igazolható monoton csökkenő függvények esetében is.
- Alkalmazzuk az "éles" egyenlőtlenségeket 1.-ben a irányban.
A konvexitás és a kétszeres derivált kapcsolata
Kimondás
Legyen egy nyílt intervallum. Tegyük fel, hogy . Ekkor
- konvex [vagy konkáv] -n [vagy ] -n
- ha [vagy ] -n szigorúan konvex [vagy szigorúan konkáv] -n
Bizonyítás
Az alábbi ekvivalens állítások érvényesek:
- konvex -n -n
- szigorúan konvex -n -n
- konkáv -n -n
- szigorúan konkáv -n -n
Ezek alapján a tétel állítása a monotonitás és a derivált kapcsolatára vonatkozó tételből következik, ha azt az deriváltfüggvényre alkalmazzuk, és figyelembe vesszük azt is, hogy .
Az előző négy állításból csak az elsőt fogjuk igazolni. A többi hasonlóan igazolható.
Legyen tetszőleges és is tetszőleges. Tegyük fel, hogy konvex -n. Ekkor
Egyszerű átrendezésekkel azt kapjuk, hogy
Vegyük itt az , illetve az határátmenetet: Tehát monoton növekedő -n
Tegyük fel, hogy monoton növekvő -n. Legyen , és is tetszőleges. Ekkor a Lagrange-féle középértéktétel szerint és :
Mivel -n, ezért , vagyis
Ez az egyenlőtlenség a következő módon alakítható át:
Ez azt jelenti, hogy konvex -n.
A L'Hospital-szabály a 0/0 esetben
Kimondás
Legyen , illetve . Ekkor
- és
Bizonyítás
Csak egy esetet (véges) bizonyítunk.
Legyen . Azt kell igazolni, hogy azaz
Az feltétel azt jelenti, hogy
Értelmezzük az és a függvényt az pontban úgy, hogy
A feltételből következik, hogy ekkor
Legyen egy tetszőleges rögzített szám, és a -ben szereplő szám.
Legyen , és egy tetszőleges pont.
A Cauchy-féle középértéktétel feltételei az és a függvényre az intervallumon teljesülnek.
Ez azt jelenti, hogy , amire
A állítást tehát bebizonyítottuk. A határérték létezik, és
A deriválhatóság ekvivalens átfogalmazása lineáris közelítéssel
Kimondás
Legyen és . Ekkor
Bizonyítás
Ha és
akkor és ezért a feltétel az választással teljesül.
Most tegyük fel, hogy és , hogy Ebből adódik, ami azt jelenti, hogy és
A Taylor-formula a Lagrange-féle maradéktaggal
Kimondás
Legyen és tegyük fel, hogy Ekkor a fenti képlet jobb oldalán álló függvényt Lagrange-féle maradéktagnak nevezzük.
Bizonyítás
A Cauchy-féle középértéktételt fogjuk felhasznáéni. Legyen
-ből következik, hogy Továbbá, , hiszen , mert egy legfeljebb -ed fokú polinom.
Másrészt, legyen . Ekkor minden esetén
amiből következik, hogy és
Tegyük fel, hogy és például . (Az eset hasonlóan vizsgálható.) Az és függvényekre az intervallumon alkalmazható a Cauchy-féle középértéktétel, következőképpen:
A Cauchy-féle középértéktételt most és a függvényekre az intervallumon alkalmazzuk:
Ha a fenti gondolatmenetet -szer megismételjük, akkor a -dik lépésben :
Az darab lépés során kaptt egyenlőségeket egybevetve azt kapjuk, hogy
hiszen minden esetén és . A konstrukcióból látható, hogy az pont és pont között van, ezért a választással a bizonyítandó állítást kapjuk.
Elégséges feltétel függvények Taylor-sorral történő előállítására
Kimondás
Legyen , és tegyük fel, hogy valós szám, amire teljesül. Ekkor -nek az ponthoz tartozó Taylor sora a halmazon előállítja az függvényt, vagyis fennáll a következő egyenlőség:
Bizonyítás
Legyen egy tetszőleges pont. Azt kell igazolni, hogy Ez a Taylor-formula szerint igaz, hiszen létezik olyan pont és között, hogy
A határozatlan integrál linearitása
Kimondás
Legyen nyílt intervallum. Ha az függvényeknek létezik primitív függvénye, akkor tetszőleges mellett -nek is létezik primitív függvénye és
Bizonyítás
Legyen és . Ekkor , illetve és .
Ekkor az említett deriválási szabályok miatt
Ez azt jelenti, hogy .
A parciális integrálás szabálya
Kimondás
Legyen nyílt intervallum. Tegyük fel, hogy és az függvénynek létezik primitív függvénye -n. Ekkor az függvénynek is van primitív függvénye és
Bizonyítás
Ha , akkor és . Mivel , illetve , ezért és Így valóban fennáll.
A második helyettesítési szabály
Kimondás
Legyenek nyílt intervallumok. Tegyük fel, hogy -n (vagy -n) és az függvénynek van primitív függvénye. Ekkor az függvénynek is van primitív függvénye és
Bizonyítás
Ha -n, akkor szigorúan monoton növekvő, és ha -n, akkor szigorúan monoton csökkenő. Mindkét esetben invertálható, és mivel folytonos és -n, így az inverz függvény deriváltjára vonatkozó tétel szerint a függvény differenciálható minden pontjában, és
Legyen , akkor és . Ekkor az összetett függvény deriválására vonatkozó tétel szerint és
Ez azt jelenti, hogy , amiből a tétel állítása következik.
Az integrálfüggvény folytonossága
Kimondás
Legyen és az függvény pontban
eltűnő integrálfüggvénye.
Ekkor .
Bizonyítás
Mivel , ezért az korlátos függvény, így , hogy
Legyen egy tetszőleges pont és olyan sorozat, hogy .
Tegyük fel, hogy . Ekkor a határozott integrál tulajdonságai alapján
Ezért az átviteli elv szerint jobbról folytonos az pontban. Hasonlóan igazolható, hogy balról folytonos az pontban.
Az integrálfüggvény deriválhatósága
Kimondás
Legyen és az függvény pontban eltűnő integrálfüggvénye. Tegyük fel, hogy olyan pont, amire f \in C{\x} teljesül. Ekkor és .
Bizonyítás
Legyen olyan szám, amire teljesül. Ekkor a határozott integrál tulajdonságai alapján
Másrészt, mivel egy rögzített szám, így
Ezért az integrál linearitása alapján
Mivel , így a definíció szerint
Legyen . Ekkor . Így a fentiek és az integrál tulajdonságai szerint
Így
Hasonlóan igazolható, hogy létezik bal oldali deriváltja az pontban, és .
Így
A Newton-Leibniz-formula
Kimondás
Tegyük fel, hogy
- és
- az függvénynek van primitív függvénye az intervallumon.
Ekkor ahol az függvény egy primitív függvénye.
Bizonyítás
Legyen , és tekintsük az intervallum egy tetszőlegesen megválasztott felosztását. A Lagrange-féle középértéktétel szerint minden indexre van olyan pont, amelyre
teljesül. Ha ezeket az egyenlőségeket összeadjuk minden indexre, akkoe a bal oldalon minden tag kiesik, kivéve az és az tagokat. Így azt kapjuk, hogy
Mivel , ha , ezért a
egyenlőtlenség minden felosztásra teljesül. Következésképpen
Az (azaz az ) feltételből így az következik, hogy
Egy vektorsorozat és koordinátasorozatai konvergenciájának kapcsolata
Kimondás
Legyen . Egy -beli sorozat akkor és csak akkor konvergens, ha a sorozat minden koordinátasorozata konvergens, és a határértéke a határvektor megfelelő koordinátája, azaz
pontosan akkor igaz, ha minden koordinátára
Bizonyítás
Tegyük fel, hogy , azaz .
Rögzítsük az indexet. Mivel
ezért a közrefogási elv szerint , azaz
Tegyük fel, hogy minden indexre , azaz Ekkor az egyenlőtlenség és a közrefogási elv alkalmazásával az kapjuk, hogy ha , azaz .
A deriváltmátrix egyértelműsége
Kimondás
Tegyük fel, hogy és . Ekkor az deriváltmátrix egyértelműen mehatározott.
Bizonyítás
Tegyül fel, hogy az és mátrixko kielégítik a totálisan deriválhatóság definíciójában szereplő feltételeket. Ekkor
A közrefogási elv miatt
Így , azaz minden esetén. Tehát a mátrixok mindegyik -edik oszlopa megegyezik, és így .
A deriváltmátrix előállítása
Kimondás
Legyen , ahol az függvény -edik koordinátafüggvénye. Ha , akkor a Jacobi-mátrix.
Bizonyítás
mátrix, hogy Az függvény -edik koordinátafüggvényére a választással azt kapjuk, hogy A parciális derivált értelmezése alapján tehát
A totális- és az iránymenti derivált kapcsolata
Kimondás
Tegyük fel, hogy és . Ekkor minden irányban vett iránymenti deriváltja létezik az pontban, és
az úgynevezett gradiensvektor és egységvektor, azaz
Bizonyítás
Ha , akkor , úgy, hogy
Legyen . Ekkor , hiszen , és így
Ezért
hiszen a függvény korlátos és .
típusú függvényekre vonatkozó elsőrendű szükséges feltétel a lokális szélsőértékre
Kimondás
Tegyük fel, hogy és . Továbbá
- és
- az függvénynek az pontban lokális szélsőértéke van.
Ekkor , azaz .
Bizonyítás
Legyen rögzített és tekintsük meg a valós-valós parciális függvényt! Ekkor
- ha , akkor , és azt is tudjuk, hogy és .
- ha -nek az pontban lokális szélsőértéke van, akkor , hogy -nek az pontban abszolút szélsőértéke van a környezetben. Azonban ami azt jelenti, hogy -nek az pontban abszolút szélsőértéke can az környezetben, azaz -nek az pontban lokális szélsőértéke van.
Ekkor a valós-valós függvényeknél tanult, a lokális szélsőértékre vonatkozó elsőrendű szükséges feltétel szerint , ami éppen azt jelenti, hogy
típusú függvényekre vonatkozó másodrensű elégséges feltétel a lokális szélsőértékre
Kimondás
Legyen és . Tegyük fel, hogy
- az Hesse-féle mátrix pozitív (negatív) definit.
Ekkor az függvénynek az pontban lokális minimuma (maximuma) van.
Bizonyítás
A Peano-féle maradéktagos Taylor-formula szerint van olyan a feltételnek eleget tevő függvény, hogy
Ha és akkor a fenti egyenletből:
Ha az mátrix, vagyis a kvadratikus alak pozitív definit, akkor és
A egységvektor, tehát
Ezért
Mivel , így . Ha , akkor
Az helyettesítéssel azt kapjuk, hogy
ami azt jelenti, hogy az függvénynek lokális minimuma van az pontban.
Hasonlóan igazolható, hogy ha negatív definit, akkor az függvénynek lokális maximuma van az pontban.
típusú függvényekre vonatkozó másodrendű szükséges feltétel a lokális szélsőértékre
Kimondás
Legyen és . Ha az függvénynek az pontban lokális minimuma (maximuma) van, akkor
- az Hesse-féle mátrix pozitív (negatív) szemidefinit.
Bizonyítás
Az elsőrendű szükséges feltétel miatt . A Hesse-féle mátrixszal kapcsolatos állítás igazolásához tegyük fek, hogy -nek az pontban lokális minimuma van (lokális maximum esetén hasonlóan igazolható). Így környezet, hogy minden esetén. Rögzítsünk egy tetszőleges pontot. Ekkor
A Peano-féle maradéktagos Taylor formula szerint vaon olyan , a feltételnek eleget tevő függvény, hogy
Ha és akkor a fenti egyenletből:
ezért
Ekkor
Ez azt jelenti, hogy a kvadratikus alak, illetve az mátrix pozitív szemidefinit.
Operációs rendszerek előadás
Alapadatok
Idő: Hétfő, 17:00 - 18:00
Helyszín: Déli Tömb 0-822 Mogyoródi József Terem
Oktató: Dr. Illés Zoltán, zoltan.illes@elte.hu
Csoport: 91
Értékelés
- 2 beadandó
- 2 ZH
- 1.ZH: 12. hét, az előadás anyaga
- 2.ZH: Utolsó hét, előadás és gyakorlat anyaga
Források
- Windows Internals
- Knapp Gábor, Adamis Gusztáv: Operációs rendszerek
- Andrew S. Tanembaum, Herbert Boss: Modern Operating Systems
- Andrew S. Tanembaum, Albert S. Woodhull: Operációs rendszerek
1. Előadás
Tematika
- Bevezetés, előzmények (számítógépes alapismeretek, számítógépek felépítése,API)
- Operációs rendszer fogalma, fejlődése, felhasználói felület
- Fájlok, könyvtárak, lemezkezelés
- Folyamatok, ütemezések
- Bevitel-kivitel, erőforrások, holtpontok kezelése
- Memóriakezelés
- Real-Time Operációs rendszer jellemzők
- Suse Linux Enterprise szerver esettanulmány
- Windows Core, Azure, Felhő
Források
2. Előadás
Számítógépek hardveres felépítése
- Tárolt programok, utasítások adatok azonos módon a memóriában helyezkednek el.
- Vezérlő egység (CPU), aretmetikai-logikai egység (ALU) az utasítások végrehajtását, alapvető aritmetikai műveleteket felügyelik.
- Szükség van be/kimenetek (I/O) kezelésre.
- Összekötő kapocs: busz (sín, adat, cím, vezérlő)
Processzor utasítások
A rendszer gyakorlatilag minden eleme intelligens, de a kulcsszereplő a processzor, mikrokontroller.
Regiszterek: speciális memória a processzoron belül. (általános, jelző, )
Utasításcsoportok:
- Adatmozgató utasítások
- Ugró utasítások (abszolút, relatív)
- I/O port kezelés
- Megszakítás kezelés
Védelmi szintek
- Kernel mode (interrupt, I/O, bizonyos memória kezelése)
- User mode
Adatok, utasítások a memóriában, ezeket a CPU végrehajtja.
Számítógépek szoftveres felépítése
- Logikai áramkörök
- CPU, mikroprogram, mikroarchitektúra szint
- Számítógép, gépi elemek gépi kódja
- Operációs rendszer
- Rendszeralkalmazások
- Alkalmazások
Operációs rendszer fogalma, feladata
Operációs rendszer: Olyan program ami egyszerű felhasználói felületet nyújt, eltakarva a számítógép(rendszer) eszközeit.
- Absztrakt, virtuális gép
- pl.: mindegy hogyan, de át akarok másolni egy képet.
- Erőforrás menedzser
- Felhasználói felület biztosítása
- Kommunikáció perifériákkal
- Lekérdezéses átvitel (polling): I/O portok folyamatos lekérdezése
- Interrupt használat: A kívánt esemény bekövetkezésekor a megadott programrész kerül végrehajtásra.
- DMA, közvetlen memória elérés
Programkönyvtárak
Lehetnek gépi kódban írtak, de leggyakrabban C-API-t biztosítanak.
Jellemzően réteges szerkezetű:
- Rendszer szintű hívás (pl.: kommunákció a perifériákkal)
- Felhasználói hívás
Firmware: Hardverbe a gyártó által épített szoftver
Middleware: OS feletti réteg, pl.: JVM
POSIX
POSIX = Portable Operating System Interface for uniX (IEEE 1003, ISO 9945)
Valójában egy minimális rendszerhívás API.
Szabvány ANSI C-vel azonos függvénykönyvtár.
Manapság mindens OS POSIX kompatibilis.
Fontosabb POSIX témakörök:
- Fájl, könyvtárműveletek
- Folyamatok kezelése
- Szignálok
- Csövek
- Standard C függvénykönyvtár
- Órák, időzítők
- Szálak kezelése
Függvénycsoport példák
- Matematikai függvények: pl. sin, cos, tan, atan, atan2, log, exp stb.
- Állománykezelő függvények: pl. creat, open, fopen, close, read, write, unlink stb.
- Könyvtárkezelő függvények: pl. opendir, closedir, mkdir, rmdir, readdir stb.
- Karakterfüzér‐kezelő függvények: strcpy, strlen strcmp, strcat, strchar, strstr stb.
- Memória-kezelők: malloc, free, memcpy stb.
- Belső kommunikációs függvények: msgsnd, msgrcv, shmat, semop, signal, kill, pipe stb.
Források
3. Előadás
Operációs rendszer generációk
- Történelmi generáció, tisztán mechanikus, nincs oprendszer
- Első generáció (1940-1955), kapcsolótála, relé, vákumcső
- Egedi gépek
- Neumann modell
- Gépi kód
- Lyukkártya
- Második generáció (1955-1965) tranzisztoros rendszerek
- Megbízható elemk
- Géptermek (mainframe)
- Szalagos egységek, üzemeltetési fázisok elkülönítése
- FORTRAN nyelv
- Oprendszerek
- Harmadik generáció (1965-1980), intrgrált áramkörök
- Azonos rendszerek, felépítések, kompatibilitás
- Multiprogramozás, multitask megjelenése
- Spooling, időosztás
- 1980-napjainkig személyi számítógépek, Windows
- Large Scale Integration áramkörök, CPU fejlődés
- Hálózati osztott rendszerek
- GUI
MINIX 3
AT&T engedélye alapján használható volt
Linus Torvalds fejlseztette ez alapján a Linuxot.
Rendszerhívások
Azok a szolgáltatások, melyek az operációs rendszer ésa felhasználói programok közti kapcsolatot biztosítják.
Két csoportja:
- Folyamat kezelő csoport
- Fájlkezelő csoport
Process kezelés
Processz: végrehajtás alatt lévő program
- Saját címtartomány
- Processz táblázat (cím, register)
- Processz indítás, megszüntetés
- Processz felfüggesztés (memóriatérkép + táblázat mentés)
- Processzek kommunikációja (signalok)
Fájlkezelés
Egy főkönyvtár, fastruktúra (fájl, könyvtár)
Jogosultságok, műveletek
Speciális fájlok: adatcső
Operációs rendszer struktúrák
Monolitikus rendszerek
Rendszerkönyvtár egyetlen rendszer, így mindenki mindenkit láthat.
Információelrejtés nem igazán van.
Rendszerhívás során gyakran kernel módba kapcsolja a CPU-t
Rétegelt szerkezet
- Gépkezelő
- Felhasználói programok
- I/O kezelés
- Gépkezelő-folyamat
- Memória és dobkezelés
- Processzorhozzáférés és multiprogramozás
Kliens/szerver modell
Felhasználói program: kliens program Kiszolgáló program: szerver program
Mindegyik felhasználó módban fut egyre kevesebb funkció marad a kernelben
Virtuális gépek
Eredetileg az IBM-től származik az ötlet Virtuális gép monitor: a hardvert pontosan másolja Ezt tetszőleges példányban képes volt sokszorozni
Virtualizációs fogalmak
- host rendszer
- paravirtualizáció - vendég rendszerben módosítják a kritikus utasításokat, ma már nem igazán használt.
- szoftveres virtualizáció
- hardveres virtualizáció
- konténerizáció
Operációs rendszer elvárások
- Hatékonyság
- Megbízhatóság
- adatok megőrzése
- rendelkezésre állás
- hibatűrés
- Biztonság
- Kompatibilitás, hordozhatóság
- Alacsony energia felhasználás
- Rugalmasság
- Kezelhetőség
Források
4. Előadás
Háttértárak
- Mágneses
- Mágnesszalagok
- Mágneslemezek
- Merevlemez
- Floppy
- Optikai
- CD, DVD, Blu-Ray
- Félvezető (flash)
- USB drive, memóriakártya
- SSD
Mágnesszalag fizikai felépítése
- Lineáris felépítés
- 9 bites keret (8bit + paritás)
- Keretek rekordokba szerveződnek
- Rekordok között: rekord elválasztó (record gap)
- Egymás utáni rekordok után, fájl elválasztó (file gap)
- Szalag elején könyvtárszerkezet
- Jellemző használat:
- Biztonsági mentés
- Nagy mennyiségű adattárolás
- Nem igazán olcsó
Mágneslemezek felépítése
- FDD - Floppy Disk Drive
- jellemzően egy lemez
- HDD - Hard Disk Drive
- jellemzően több lemez
- Kör alakú lemez - sávos felosztás
- Sávok szektorokra oszthatók - blokk
- Klaszter - több blokk
- Több lemez - egymás alatti sávok: cilinder
- Logikailag egy folytonos blokksorozat
- A fizikai működést a meghajtó (firmware) eltakarja.
Címzés: CHS (Cilinder-Head-Sector), LBA (Logical Block Addressing)
Optikai tárolók
- 8 vagy 12 cm átmérőkű optikai lemezek
- Működési elv: Fény visszaverődés idő különbség alapján.
- Belső résztől spirális "hegyek - völgyek" (pit-land) sorozata.
- Írás: fény törésmutatóját változtatja meg, így más lesz a fény terjedési sebessége.
Eszközmeghajtó
- Az a program, amely a közvetlen kommunikációt végzi.
- A kernelnek, az operációs rendszer magjának része.
- A lemezek írása-olvasása során jellemzően DMA-t használnak
- Megszakítás üzenet, tipikusan azt jelzi, ha befejeződött az írás-olvasás művelet
- I/O portokon az írás, olvasási paraméterek beállítását végzik.
- Réteges felépítés
Formázás
Mágneslemez formázása
- Sávos-szektoros rendszer kialakítása
- Jellemzően egy szektor 512 byte
- Gyárilag a lemezek "elő vannak készítve"
- Quick format - Normal format
- A normál hibás szektorokat keres.
- Szektor = Szektorfej + adatblokk + lábléc
- Szektorfej: sáv száma, fej száma, szektor száma
- Lábléc: hibajavító blokk
- A szektorok kialakítását alacsonyszintű formázásnak nevezzük.
Logikai formázás
- Partíciók kialakítása
- Egy lemezen, több logikai lemezrész kialakítható (PC-s rendszeren 4)
-
- szektor - MBR (Master Boot Record)
- 2 részből áll, 512 bájt
- Bootloader (446 bájt)
- Max 4 partíció adatai (4x 15 bájt)
- 2 bájt, mindig 0x55 0xAA
- Elsődleges partíció - erről tölthető be az operációs rendszer
- Kiterjesztett partíció - több logikai meghajtó lehet
- Swap partíció
- UEFI esetén is létezik - Protektív MBR-es teljes méretet megadó partíciós bejegyzés-
- A partíción a szükséges adatszerkezet kialakítása.
Boot folyamat
- ROM-BIOS megvizsgálja, lehet-e operációs rendszert betölteni, ha igen betölti a lemez MBR programját a 7c00h címre.
- Egy elsődleges partíció lehet aktív, az MBR programja megvizsgálja melyik az.
- Az aktív partíció boot szektorát (1. szektor) betölti a memóriába.
- Ez már a partícióra installált operációs rendszer betöltő programja Pl. LILO, NTFS boot
- A boot program tudja, hogy a partíció melyik fájljait kell a memóriába tölteni, majd elindít egy „rendszerstartot”
- Többszintű folyamat, rendszerfüggő.
UEFI vs Legacy vs BIOS
- BIOS probléma: MAX. 2TB háttértár kezelés
- Basic Input-Output System, IBM PC alap firmware
- UEFI (BIOS utód) – Unified Extensible Firmware
Interface
- BIOS x86 valós módban fut mindenhol, UEFI natívban (x86- 32, x64)
- 2TB-nál nagyobb meghajtók, 128 partíció, nagyobb RAM
- MBR nem használt, helyette GPT (GUID Partition Table)
- OS betöltő saját fájlrendszerben .efi kiterjesztés
- Csak 64 bites OS betöltő!
- Secure boot(csak digitálisan aláírt driverek, OS boot betöltő engedélyezés)
- Általános boot lehetőségek: Legacy boot (BIOS), UEFI boot, Dual (Compatibility Support Module)
UEFI GPT táblázat
- Az MBR (0.szektor) Protective MBR, 0xEE GPT típus az egész lemez méretre vonatkozik
-
- szektor- GPT fejléc (header) , lemez GUID, stb.
-
- szektortól- 32 szektor, 128 byte egységenként a partíciós bejegyzések (Partition Entry Array)
- 128 partíció, 128/4=32
- Partíció végén a partíciós bejegyzések másolata és a fejléc másolata.
Források
5. Előadás
Lemez elérés fizikai jellemzői
- Forgási sebesség (ma tipikusan 5400-15000/perc)
- Fej mozgási sebesség
- Az írás olvasás ütemezés feladata a megfelelő kiszolgálási sorrend meghatározása.
- Válaszidő csökkentése
- Sávszél növelése
I/O műveletek
- Alacsonyszintű hívás során az alábbi adatok szükségesek:
- Beolvasandó (írandó) blokkok sorszáma
- Memóriaterület címe, ahova be kell olvasni
- Bájtok száma
Ütemezés
- Alacsonyszintű (kernel) feladat paraméterek
- Kérés típusa (írás-olvasás)
- A blokk kezdőcíme (LBA cím vagy sáv, szektor, fej száma)
- DMA memoriacím
- Mozgatandó bájtok száma
- Több folyamat is használná a lemezt?
- Ütemező feladata: Kit szolgáljunk ki elősször?
- Fejmozgás figyelembevétele
Sorrendi ütemezés (FCFS)
- First Come - First Serve
- Ez a legegyszerűbb stratégia
- Biztosan minden kérés kiszolgálásra kerül
- Nem törődik a fej aktuális helyzetével
- Nem igazán hatékony
- Kicsi az sávszél
- Átlagos válaszidő, kis szórással
SSTF ütemezés
- Shortest Seek Time First
- A legkisebb fejmozgást részesíto előnyben
- Átlagos várakozási idő kicsi, de szórása nagy
- Átviteli sávszél nagy
- Fennáll a kiéheztetés veszélye
Pásztázó ütemezés
- SCAN módszer
- A fej állandó mozgásban van, és a mozgás útjába eső kéréseket kielégíti
- A fej mozgás megfordul, ha a mozgás irányában nincs kérés, vagy a fej szélső pozíciót ért el
- Rossz ütemben érkező kérések kiszolgálása csak oda-vissza mozgás után kerül kiszolgálásra.
- Várakozási idő közepes, szórás nagy
- Középső sávok elérés szórása kicsi
Egyirányú pásztázás
- Circular SCAN, C-SCAN
- A SCAN javítása, írás-olvasás, csak a fej egyik irányú mozgásakor történik.
- Gyorsabb fejmozgás
- Nagyobb sávszélesség
- Az átlagos várakozási idp hasonló, mint a SCAN esetén, viszont a szórás kicsi
Ütemezés javítások
-
FCFS módszernél, ha az aktuális sorrendi kérés kiszolgálás helyén van egy másik kérés blokkja, akkor szolgáljuk ki azt is.
-
Egy folyamat adatai jellemzően egymás után vannak, így egy kérés kiszolgálásánál várva egy kicsit, a folyamat az adatainak további részét is kéri a folyamat.
- Előlegező ütemezésnek is nevezzük
-
A lemez közepe általában hatékonyan elérhető
-
A DMA maga is memória
-
Memória buffer használata:
- Kettős körszerű használat
- Olvasás: Ütemező tölti, felhasználói folyamat üríti
- Írás: Felhasználó folyamat tölti, ütemező üríti
-
Disc cache
- Előre dolgozik az ütemező, a memóriába tölti a kért adatok "környéki" lemezterületet is
- Operációs rendszernek jelent plusz feladatot
SLE Block device ütemezés
- CFQ - Completely Fair Queuing
- Minden folyamat saját I/O sort kap.
- Ezen sorok között azonosan próbálja az ütemező elosztani a sávszélességet
- Ez az alapértelmezett ütemező
- Létezik még:
- NOOP: Egy sor van, amit a (RAID) vezérlők gyorsan teljesítenek
- Deadline: egy kéréshez határidő tartozik, két sort használ. Egy blokksorrend alapján készített sort (SSTF) és egy határidő alapján készített sort. Alapból a blokksorrend a lényegesm de ha határidő van, akkor az kerül sorra
Ütemezés választás
- A fenti algoritmusok csak a fejmozgás idejét vették figyelembe, az elfordulást nem.
- A sorrendi ütemezés tipikusan egy felhasználós rendszernél használt
- SSTF, kiéhezés veszélye nagy
- C-SCAN, nagy IO átvitel, nincs kiéheztetés
- Beépített ütemező: Pl.: SCSI vezérlők
Ütemezés kulcsfeladata
- Minél gyorsabban kiszolgálni a kéréseket.
- Ezt mi is segíthetjük:
- Összetartozó adatok együtt legyenek
- Sávszélesség a lemez közepén a legnagyobb
- Leggyorsabban a lemez közepét érhetjük el
- Lemez gyorsító tár a memóriában
- Adattömörítés
Lemezek megbízhatósága
- Az adatok redundás tárolása, hogy lemezsérülés esetén se legyen adatvesztés
- Operációs rendszer szolgáltatás
- Dinamikus kötet: több lemezre helyez egy logikai meghajtót, méret összeadódik
- Tükrözés: két lemezre helyez egy meghajtót, mérete az egyik lemez mérete lesz
- Hardware szolgáltatás:
- Intelligens meghajtó szolgáltatás
- A SCSI eszköz világában jelent meg elősször (RAID)
RAID
- Ha az oprendszer nyújtja, gyakran SoftRaid-nek nevezik.
- Több lemezt fog össze, és egy logikai egységként látja az operációs rendszer
- Több "összefogási" elv létezik: RAID 0-6
RAID 0 (striping)
- Nem redundáns
- Több lemez logikai összefűzésével egy meghajtót kapunk
- A lemezkapacitások összege adja az új meghajtó kapacitását
- A logikai meghajtó blokkjait szétrakja a lemezekre (striping), ezáltal egy fájl írása több lemezre kerül.
- Gyorsabb I/O műveletek
- Nincs meghibásodás elleni védelem
RAID 1 (mirroring)
- Két független lemezből készít egy logikai egységet
- Minden adatot párhuzamosan kiír mindkét lemezre
- Tárolókapacitás felére csökken
- Drága megoldás
- Jelentős hibatűrő képesség
RAID 1+0, RAID 0+1
- RAID 1+0: Tükrös lemezekből vonunk össze többet
- RAID 0+1: RAID 0 összevont lemezekcsoportokból vegyünk kettőt
- A vezérlők gyakran nyújtják egyiket, másikat, mivel így is, úgy is tükrözés van, azaz drága, így ritkán használt.
RAID 2,3,4
- RAID 2: Adatbitek mellett hibajavító biteket is tartalmaz, pl.: 4 lemezhez 3 javító lemez
- RAID 3: Elág egy plusz paritáslemez, n+1 lemez
- RAID 4: RAID 0 kiegészítése paritáslemezekkel
- Ma ezen megoldások nem gyakran használatosak
RAID 5
- Nincs paritáslemez, ez el van osztva a tömb összes elemére
- Adatok is elosztva ketülnek tárolásra
- Intenzív vezérlő CPU igény
- Redundáns tárolás, 1 lemez meghibásodása nem okoz adatvesztést
- N lemez RAID 5 tömbben, N-1 lemez méretű logikai meghajtót ad
RAID 6
- A RAID 5 paritásblokkhoz, hibajavító kód kerül tárolásra (+1 lemez)
- Még intenzívebb CPU igény
- Két lemez egyidejű kiesése sem okoz adatvesztést
- N lemez RAID 6-os tömbjének kapacitása N-2 lemez kapacitásával azonos
- Elvileg általánosítható módszer X lemez kiesésére
Források
6. Előadás
- 6. Előadás
- Fájlrendszer
- Fájl
- Könyvtár
- Hozzáférési jogok
- Fájlok elhelyezése
- Könyvtár megvalósítása
- Fájlnév tárolás
- Lemez kvóták
- Megosztott fájlok
- Titkosított fájlrendszer
- Mentések
- Fájl, könyvtár műveletek
- Fájlrendszer típusok
- Naplózott fájlrendszerek
- Fájlrendszer támogatás
- Különböző fájlrendszerek együttes használata egy gépen
- Alkalmazás és lemez kapcsolat
- FAT
- UNIX könyvtárszerkezet
- NTFS
- Források
- Fájlrendszer
Fájlrendszer
- Fájl: adatok egy logikai csoportja, névvel egyéb paraméterekkel ellátva.
- Könyvtár: fájlok (könyvtárak) logikai csoportosítása.
- Fájlrendszer: módszer, a fizikai lemezünkön, kötetünkön a fájlok és könyvtárak elhelyezés rendszerének kialakítására.
Fájl
-
A fájl az információtárolás egysége.
-
Névvel hivatkozunk rá.
-
Jellemzően egy lemezen helyezkedik el, de általánosan az adathalmaz, adatfolyam akár képernyőhöz, billentyűzethez is köthető.
-
A lemezen általában 3 féle fájl, állomány található:
- Rendes, normál felhasználói (alkalmazói) állomány.
- Ideiglenes állomány
- Adminisztratív állomány. Ez a működéshez szükséges, általában rejtett.
-
Fájlnév: Karaktersorozat
- Operációs rendszer függvénye, hogy milyen a szerkezete(hossza, megengedett karakterek, kis- nagybetű különbözőség)
-
Egyéb attribútumok (információ):
- Mérete, tulajdonosa, utolsó módosítás ideje, rejtett (hidden) fájl-e, rendszer fájl-e, hozzáférési jogosítványok, tulajdonos,
-
Fizikai elhelyezkedés:
- Valódi fájl, link (hard), link (soft)
Könyvtár
- Valójában egy speciális bejegyzésű állomány, tartalma a fájlok nevét tartalmazó rekordok listája.
- Könyvtár szerkezetek
- Katalógus nélküli rendszer, szalagos egység
- Egyszintű, kétszintű katalógus rendszer (nem igazán használt)
- Többszintű, hierarchikus katalógus rendszer
- Fa struktúra
- Hatékony keresés
- Ma ez a tipikusan használt.
- Abszolút, relatív hivatkozás
- PATH környezeti változó
Hozzáférési jogok
- Nincs általános jogosítvány rendszer
- Jellemző jogosítványok:
- Olvasás
- Írás, létrehozás, törlés
- Végrehajtás
- Módosítás
- Full control
- Jogok nyilvántartása:
- Attribútumként
- ACL
- NFS-AFS különbözőség, hasonló elv, különböző implementáció
Fájlok elhelyezése
- A partíció elején, az un. Szuperblokk (pl. FAT esetén a 0. blokk ) leírja a rendszer jellemzőit.
- Általában következik a helynyilvántartás (FAT, láncolt listás nyilvántartás)
- Ezután a könyvtárszerkezet (inode), a könyvtár bejegyzésekkel, fájl adatokkal. (FAT16-nál a könyvtár előbb van, majd utána a fájl adatok.)
Folyamatos elhelyezésű
- First Fit (első szabad hely, ahová befér)
- Best Fit (arra a helyre, ahol a legkevesebb szabad hely marad)
- Worst Fit (Arra a helyre illesztjük, ahol a legtöbb szabad hely marad)
- Mindegyik veszteséges.
Láncolt tárolás
- Nincs veszteség (csak a blokk méret).
- A fájl adatai egy láncolt blokk listában vannak.
- Az utolsó blokk elérése lassú.
- Szabad-foglalt blokkok: File Allocation Table, FAT
- Nagy méretű lehet és a FAT mindig a memóriában van!
Indextáblás elhelyezés
- A könyvtár katalógus a file node-ok címét tartalmazza
- Az inode cím mutat a fájl adatokra.
Könyvtár megvalósítása
- A fő funkciója, hogy a névből meghatározza az adatok helyét. (keresés: lineáris, hash táblás, cache- elt)
- A könyvtárbejegyzés tartalmazhatja a:
- A címét a teljes fájlnak (folyamatos elhelyezésnél)
- Az első blokk címét (láncolt listánál)
- Az i-node számot.
- Hogyan tárolja az attributumokat?
- Bejegyzések hossza azonos, rögzített
- i-node-okban
Fájlnév tárolás
- Korábban – fix hosszúságú (8+3)
- Ma – általában max 255 karakter hosszú
- Helytakarékos megoldások:
- Különböző hosszúságú bejegyzések. Az első helyen a bejegyzés hossza, majd az attribútumok, majd a név.
- Egyforma hosszú bejegyzések, mutató a fájlnévre.
Lemez kvóták
- A felhasználói
felnyitáskor
- Megnyitja a fájl táblát a memóriában
- A kvóta táblát a memóriában
- Ha új blokkot foglal -> változik a kvóta tábla
- Bejelenkezéskor ellenőrzés
- Szoft limit átlépésekor bejelentkezhet (kivéve túllépte a lehetséges figyelmeztetések számát)
- Hard limit átlépésnél – be sem jelentkezhet
Megosztott fájlok
- Megoldandó, hogy mindenki számára minden változás látszódjon!
- Két módszer használatos:
- A fájl blokkjai egy struktúrában találhatóak és erre mutat a könyvtárbejegyzés (nem a blokkok maguk vannak felsorolva a bejegyzésben) (pl. UNIX, i-node) A user1 és user2 ugyanarra a struktúrára mutat. (Mi történik törlésnél?)
- Új link fájl létrehozásával. (symbolic link) (lassú elérés.)
Titkosított fájlrendszer
- CPU támogatás
- AES-NI (New Instructions) utasításkészlet
- Szimmetrikus kulcs
- Windows 2000 óta létezik NTFS-ben (EFS)
- Windows Jelenleg: Bitlocker
- Beépített win10 prof.
- Checkpoint Pointsec- független titkosító
- Linux – dm-crypt
- 2.6.4 kernel óta, alapértelmezett titkosítás
Mentések
- Fizikai mentés(Full backup) (mindent lemásol)
- Előny (simple, quick)
- Hátrány (felesleges mentés, pl. szabad blokkok..)
- Logikai mentés (csak a módosítottat menti)
- Előny (Igény esetén egy adott fájl vagy könyvtár is
visszaállítható nemcsak az egész) - Hátrány (bonyolult algoritmus)
- Előny (Igény esetén egy adott fájl vagy könyvtár is
- Vegyes használat
- Időnként fizikai mentés
- Sűrűbben logikai mentés
- Visszaállítás (fizikai mentés, első logikai mentés, …., utolsó logikai mentés
Logikai mentés
-
A UNIX rendszerekben gyakran használt algoritmus
- Minden módosított fájl és minden könyvtár megjelölése
- Eltávolítjuk azokat a könyvtár jelöléseket, amelyekben
(vagy amelyek alkönyvtáraiban) nem volt módosítás. - Mentjük a megjelölt könyvtárakat attribútumokkal).
- Mentjük a megjelölt fájlokat attribútumokkal.
-
A szabad blokk lista nem fájl (nincs mentve). (Visszaállítható, hiszen a komplementere a foglaltaknak.)
-
Linkek – minden könyvtárban, ahol a módosított állományra volt link, azt vissza kell állítani.
-
A fájlok lyukakat tartalmazhatnak (pl. seek+write) – Visszaállításnál a nem használt helyeket nem kell lefoglalni!
-
Nem valódi fájlokat pl. nevesített csővezetékeket nem kell menteni.
Fájl, könyvtár műveletek
- Fájl
- Megnyitás
- Műveletek: Írás, olvasás, hozzáfűzés
- Lezárás
- Adatok
- Bináris- bájt sorozat
- Szöveges- karakter sorozat
- Elérés módja, szekvenciális, random
- Könyvtár műveletek
- Létrehozás, tartalom listázása, állomány törlés
Fájlrendszer típusok
- Merevlemezen alkalmazott fájlrendszer
- FAT, NTFS, EXT2FS, XFS, stb.
- Szalagos rendszereken (elsősorban backup) alkalmazott
fájlrendszer
- Tartalomjegyzék, majd a tartalom szekvenciálisan
- CD, DVD, Magneto-opto Disc fájlrendszere
- CDFS, UDF (Universal Disc Format), kompatibilitás
- RAM lemezek (ma már kevésbé használtak)
- FLASH memória meghajtó (FAT32)
- Hálózati meghajtó
- NFS,AFS
- Egyéb pszeudó fájlrendszerek:
- Zip, tar.gz, ISO
Naplózott fájlrendszerek
- Fájlrendszer sérülés, áramszünet stb. esetén inkonzisztens állapotba kerülhet.
- Gyakran nevezik: LFS-nek (Log-structured File System) vagy JFS-nek(Journaled)
- Adatbázis kezelők mintájára: művelet + log
- Tranzakciós alap
- Leállás, hiba esetén a log alapján helyre lehet állítani.
- Célszerűen a log másik lemez (másik partíció)
- Nagyobb erőforrás igény- nagyobb megbízhatóság
- Adatmódú – Metaadat alapú naplózás
Fájlrendszer támogatás
- Mai operációs rendszerek "rengeteg" típust
támogatnak
- PL: Linux 2.6 kernel több mint 50-et.
- Fájlrendszer csatolása
- Mount, eredményeképpen a fájlrendszer állományok elérhetők lesznek.
- Automatikus csatolás (pl. USB drive)
- Kézi csatolás (Linux, mount parancs)
- Külön névtérben való elérhetőség (Windows)
- A,B,C,
- Egységes névtér (UNIX)
Különböző fájlrendszerek együttes használata egy gépen
- Lehetséges több különböző fájlrendszert használni
ugyanazon a gépen.
- Pl. Windows: NTFS, FAT-32, UDF (DVD,CD) stb.
- A rendszer egymástól függetlenül használja őket. Az hogy éppen melyiket kell használni, a drive betű határozza meg. (c:, a:)
- Pl. Windows: NTFS, FAT-32, UDF (DVD,CD) stb.
- Pl.:UNIX: ext2,ext3, UDF, stb.
- A modern UNIX rendszerek egységesen kezelik létrehozva egy közbülső réteget a virtuális fájlrendszert! (VFS)
Alkalmazás és lemez kapcsolat
- Réteges felépítés
- Alkalmazói szint
- Az alkalmazás, fejlesztői könyvtárak segítségével megoldja a lemezen tárolt adatok írását-olvasását.
- Szöveges, bináris fájlműveletek
- Operációs rendszer szint
- Fájlrendszer megvalósítás
- Elérhetőség, jogosultságok
- Kötetkezelő (Volume manager)
- Eszközmeghajtó (device driver)
- BIOS-ra alapozva
- Fájlrendszer megvalósítás
- Hardver eszköz szintje
- I/O meghajtó,IDE, SATA stb.
- Alkalmazói szint
FAT
-
File Allocation Table
- Talán a legrégebbi, ma is élő fájlrendszer!
-
A FAT tábla a lemez foglaltsági térképe, annyi eleme van, ahány blokk a lemezen
- Pl: Fat12, FDD, Cluster méret 12 bites. Ha értéke 0, szabad, ha nem foglalt.
- Biztonság kedvéért 2 tábla van.
-
Láncolt elhelyezés
- A katalógusban a file adatok (név stb.) mellett csak az első fájl blokk sorszáma van megadva.
- A FAT blokk azonosító mutatja a következő blokk címét.
- Ha nincs tovább, FFF az érték.
-
Rögzített bejegyzés méret, 32 bájt (max. 8.3 név)
-
System,Hidden,Archive,Read only, könyvtár attribútumok
-
A fájl utolsó módosítás ideje is tárolva van.
-
FAT16, 16 bites cluster leíró, 4 bájt (2x2) írja le a fájl kezdőblokkját
- Max. 4 GB partíciós méret (64kb blokk méretnél), jellemzően 2 GB.
- Fájl méret maximum is a 4 (2) GB.
- Külön könyvtári terület (FDD-n ez a 0. sáv)
- FDD-n 512 könyvtári bejegyzés
- HDD-n 32736 könyvtári bejegyzés (16 bit előjelesen)
-
FAT32 (1996-tól elérhető)
- 28 bites cluster leíró
- 2 TB partíciós méret (alap szektor mérettel)
-
32MB-ig, 1 cluster = 1 blokk(512bájt)
- 64 MB, 1 cluster=1KB (2 blokk), 128MB, 1 cluster=2KB
- 1 cluster max. 64 KB lehet.
-
Támogatták már a hosszú fájl neveket is
- Többszörös 8.3 részre fenntartott bejegyzésekkel.
-
Töredezettség mentesítés szükséges.
UNIX könyvtárszerkezet
- Indextáblás megoldás
- Boot blokk után a partíció szuperblokkja (fájlrendszer paraméterek)
- Ezt követi a szabad terület leíró rész.
- i-node tábla, majd gyökérkönyvtár bejegyzéssel)
- Moduláris elhelyezés, gyorsan elérhető az információ, sok kicsi táblázat, ez alkotja a katalógust.
- Egy fájlt egy i-node ír le!
- 15 rekeszből áll, első 12 a fájl blokkokra mutat.
- Ha kevés,a 13. rekesz újabb i-node-ra, ami +15 rekesz.
- Ha ez is kevés, a 14. rekesz újabb i-node-ra ami az első mintáját ismétli.
NTFS
-
New Technology File System
- FAT-NTFS hatékonysági határ: kb. 400 MB.
-
255 karakteres fájl név, 8+3 másodlagos név
-
Kifinomult biztonsági beállítások
-
Ahogy a FAT esetén, itt is szükséges a töredezettség mentesítés.
-
Titkosított fájlrendszer támogatása, naplózás
-
POSIX támogatás
- Hard link (fsutil hardlink parancs), időbélyegek, kis-nagybetűk különböznek
-
Tömörített fájl, mappa, felhasználói kvóta kezelés
-
Az NTFS csak klasztereket tart nyilván, szektort (512bájt) nem
-
NTFS partíció felépítése
- A Master Table egy táblázat
- A File System Data szintén
MFT
- NTFS partíció az MFT (Master File Table) táblázattal
kezdődik
- 16 attribútum ad egy fájl bejegyzést.
- Minden attribútum 1kb. Ha ez nem elég akkor egy attribútum mutat a folytatásra.
- Az adat is egyfajta attribútum, így egy bejegyzés több adatsort tartalmazhat. (PL: Betekintő kép)
- Elvi fájlméret 2^64 bájt lehet
- Ha a fájl < 1kb, belefér az attribútumba, közvetlen fájl.
- Nincs fájl méret maximum
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
9. Előadás
Ütemezés interaktív rendszerekben
- Garantált ütemezés
- Minden aktív folyamat arányos CPU időt kap
- Sorsjáték ütemezés
- Mint az előző, csak a folyamatok között "sorsjegyeket" osztunk szét, az kapja meg a vezérlést akinél a kihúzott jegy van.
- Arányos ütemezés
- Vegyük figyelembe a felhasználókat is. Mint a garantált, csak a felhasználókra vonatkoztatva.
Windows ütemezés elvek
- Preemtív, prioritásos
- Szál alapú
- Alap a Normal prioritási osztály
- Osztályon belül folyamat függvényben változhat az időszelet hossza
- Kiéheztetés elkerülése: Priority Boost
Linux - CFS
- Completely Fair Scheduler
- A CPU idő "fair" kiosztása, hasonlít a garantált ütemezésre
- A CPU idők nyilvántartása egy fa struktúrában, balra kisebb, balra nagyobb idejű folyamatok (red-black tree)
- Nincs direkt prioritás
- Mindenki azonos, fair módon részesül a CPU erőforrásokból, de:
- A nagyobb prioritású folyamat kisebb idő csökkenést szenved el.
- Nem kell prioritáskénti folyamat nyilvántartás
I/O eszközök vezérlése
Eszközezérlők
- Az I/O eszközt a számítógéphez kapcsoló elem az eszközvezérlő, vagy adapter.
- Video vezérlő
- Soros-párhuzamos vezérlő
- USB vezérlő
- HDD vezérlő
- CPU-eszközvezérlő kommunikációja
- Memórialeképezésű I/O, Megszakítás. DMA
Megszakítások
- Ha egy I/O eszköz "adatközlésre kész", ezt egy megszakításkéréssel jelzi.
- Szoftveres vs hardveres megszakítás
- szoftveres: gépi kódú utasítás végzu, multitask esetén trap-nek hívják
- Megszakításnak száma van
- Interrupt request level:
- minden CPU tartalmaz egy regisztert ami az aktuális IRQL értéket tartalmazza
- Egy folyamat prioritása nem azonos az IRQL értékkel
- A 0 szint a folyamatok IRQL szintje (kernel, user folyamatok is)
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
11. Előadás - ZH
12. Előadás - ZH
Operációs rendszerek gyakorlat
Alapadatok
Idő: Kedd, 15:00 - 16:00
Helyszín: Déli Tömb 2-108 (PC5)
Oktató: Bende Imre
Csoport: 12
Értékelés
- 2 évfolyam zárthelyi
-
- elméleti kvíz előadás anyagából
-
- kódolós a félév végén
-
- 2 beadandó
- Nincs rá pont, csak teljesítés a fontos
Források
C bevezető
A C nyelv alakpjait ismételtük át (argumentumok, random szám generálás, stringek)
Források
Rendszerhívások, fájlkezelés
Fontos függvények
| Függvény | Leírás |
|---|---|
stat | Fájl statisztikák |
ctime | Időkonverzió |
getpwuid | Infó az user-ről (password database-ből) |
opendir, closedir | Directory megnyitása/bezárása |
readdir | Directory olvasása (mindig a következő elemet adja vissza) |
open, close, fopen, fclose | Fájl megnyitása és bezárása |
read, write | Fájl olvasása/írása |
lseek | Fájl offset beállítása |
fgets | Egy bizonyos mennyiségű adat beolvasása |
feof | EOF-nál járunk-e? |
access | Fájl elérhetőségének/hozzáférés tesztelése |
Források
Processzkezelés
Fontos függvények
| Függvény | Leírás |
|---|---|
fork | child process létrehozása |
waitpid | vár, a míg lefut a child process |
execv | lefuttat egy process-t, nem adja vissza az irányítást (csak hiba esetén) |
system | lefuttat egy parancsot, vissza adja az irányítást |
fcntl | lock-ok kezelése |
Források
Signal
Fontos függvények
| Függvény | Leírás |
|---|---|
signal | egy megadott signal-ra meghív egy függvényt |
pause | vár, amíg nem kap signal-t |
kill | megöl egy processzt, adott kóddal |
sigaddset | sigset-hez adás |
sigdelset | sigset-ből eltávolítás |
sigemptyset | sigset kiürítése |
sigprocmask | blokkolni, vagy unblock-olni tusjuk a halmazban szereplő signalokat |
Források
5. Pipe
Fontos függvények
| Függvény | Leírás |
|---|---|
sigqueue | adatot küld a signal-al együtt |
alarm | x idő elteltével küld egy SIGALARM jelzést |
raise | saját processznek küld jelzést |
settimer | timer beállítása |
mkfifo | FIFO csővezeték létrehozása |
unlink | csővezeték megszüntetése |
pipe | író/olvasó névtelen csővezeték létrehozása |
Források
Messages, shared memory, semafor
Fontos függvények
| Függvény | Leírás |
|---|---|
ftok | kulcs létrehozása |
msgget | üzenetsor létrehozása |
msgctl | üzenetsor törlése (is) |
msgsnd | üzenet küldése |
msgrcv | üzenet fogadása |
shmget | osztott memória létrehozása |
shmat | osztott memória hivatkozást teszünk |
shmdt | osztott memória hivatkozás megszüntetése |
shmctl | osztott memória törlése (is) |
semget | szemafor létrehozása |
semctl | szemafor beállítás |
sem_open | szemafor létrehozás |
sem_post | szemafor állapot +1 |
sem_unlink | szemafor törlés |
sem_wait | szemafor állapot várás és -1 |
semop | szemafor művelet |
Források
7. Beadandó bemutatás
8. Message queue
Fontos függvények
| Függvény | Leírás |
|---|---|
mq_open | message queue létrehozása |
mq_send | üzenet küldése üzenetsoron |
mq_receive | üzenet fogadása üzenetsoron |
mq_close | üzenetsor bezárása |
Források
9. Feladatmegoldás
Források
10. Feladatmegoldás
11. Feladatmeholdás
12. Beadandó bemutatás
Szoftver mély neuronhálók alkalmazásához előadás
Alapadatok
Idő: Hétfő, 18:00 - 20:00
Helyszín: Északi Tömb -1.75 Konferenciaterem
Oktató: Varga Viktor és Kovács Bálint
Csoport: 1
Értékelés
- 3-4 canvas kvíz röpdolgozat
- Nem kötelező, de érdemes megcsinálni
- 3 kötelező házifeladat
- Szóbeli vizsga
- Szorgalmi házi feladat
Források
- Canvas
- Machine Learning — Andrew Ng, Stanford University
- "Essence of linear algebra" - 3Blue1Brown
- d2l.ai
Bevezetés a gépi tanulás feladataiba és fajtáiba
- Bevezetés a gépi tanulás feladataiba és fajtáiba
Gépi tanulás lényege
A feladat konkrét megoldási algoritmusának ismerete nélkül tanuljuk meg megoldani a feladatot.
- Mintapéldák segítségével adjuk meg, hogy mi a feladat helyes megoldása
- Egy paraméteres modellhez keresünk olyan paramétereket melyekkel a modell helyesen oldja meg a feladatot.
Milyen feladatokra alkalmazható?
- Ha közelítően optimális megoldás is megfelelő.
- Ha nem ismert konkrét algoritmus, ami megoldja a feladatot.
- Ha nem gazdaságos egyedi algoritmust fejleszteni a problémára.
- Ha a feladatot csak mintapéldák segítségével tudjuk formálisan definiálni.
Példa: Különböző objektumok pozíciójának detektálása fényképen.
Milyen feladatokra nem ideális?
- Ha a probléma hatékony megoldása ismert és könnyen algoritmizálható.
- Ha a közelítő eredmény nem elégséges.
Példák:
- Veszteségmentes tömörítés
- Rendezés
- A legtöbb pontosan definiált szabályrendszer szerint működő szoftver.
Gépi tanulási módszerek
Módszerek három főbb csoportja:
- Felügyelt tanulás
- Felügyeletlen tanulás
- Megerősítéses tanulás
Felügyelt tanulás
Adott: A tanítóminta (training set), input-címke párok halmaza
(a zárójeles felső index nem hatvány, hanem az elemeinek indexe)
Feladat: A címke (az elvárt output) minél jobb becslése az inputból.
Azaz, keresünk olyan függvényt (hipotézisfüggvény), melyre:
(a hipotézisfüggveny x inputból becsli az y címkét.)
Példa 1
Becsüljük meg az autók számát egy adott városban, ha ismerjük a város lakosságának számát.
: egy adott város lakosságának száma
: egy adott városban megtalálható autók száma

Milyen hipotézisfüggvényt keressünk? Az autók száma közel arányos a város lakosságának számával
lineáris hipotézisfüggvény:
a hipotézisfüggvény paramétere, ebben az esetben az egyenes meredeksége lesz...

Példa 2
A mintaelemek nem feltétlenül egy input és egy címkéből állnak... Becsüljük meg a képen látható emberek életkorát.
: egy kép (színes, rögzített felbontás) : a fényképen található személy életkora.
Milyen hipotézisfüggvényt keressünk?
A lineáris hipotézisfüggvény nem biztos, hogy a legjobb választás...
Helyette, használjunk egy igazán bonyolult függvényt, egy konvolúciós mély neuronhálót!

A felügyelt tanulás két fő feladata
Regresszió: Folytonos értékű címke (a címkehaémaz végtelen) \ver Y \vert = \infty Példa: Autók számának, vagy életkor becslése
Klasszifikáció: Diszkrét értékű címke (véges címkehaémaz) Példa: Mintaelemek kategorizálása, mi a foglalkozása a képen szereplő személynek?
Hogyan állapítjuk meg mennyire jó a becslés?
költségfüggvény segítségével.
A költségfüggvény megadja, hogy mennyire tér el a valódi címke és a becslésük adott paraméter értékek esetén.
Például:
Keressük azokat a paramétereket, melyekkel a hipotézisfüggvényünk jól közelíti meg a velódi címkét, azaz a költségünk minimális.
Megkeressük (tanuljuk) az optimális paramétereket a tanítóhalmazon, majd új, címkézetlen adathoz is tudunk becsülni címkét a betanított modellel.
A felügyelt tanulás alkalmazásai
- Objektumdetektálás, képszegmentálás
- : egy fénykép
- : A képen található objektumok köré írt téglalap koordinátái, az objektum kategóriái, vagy pixel szintű kategóriatérkép.
- 2D / 3D humán pózbecslés képről
- : egy fénykép
- : A képen található személyek ízületeinek 2D vagy 3D koordinátái
- Optical Flow becslés - két képkocka pixeleinek megfeleltetése egymással
- : Egy videó két egymást követő képkockája
- : Az első képkocka minden pixeléreegy-egy elmozdulásvektor, amely a második képkocka valamelyik pixelére mutat.
A felügyelt tanulás problémája:
- Az állatok / emberek általában nem szorulnak ra konkrét input-output párok jelenlétére, ahhoz, hogy tanuljanak.
- A címkézett adat előállítása nagy mértékű humán munkát igényelhet, címkézetlen adat viszont rengeteg van.
Felügyeletlen tanulás
Címke hiányában a feladat nem egyértelmű...
Többféle konkrét feladat lehetséges:
- Klaszterezés: Valamilyen hasonlósági reláció alapján a mintaelemek csoportosítása.
- Tömörítés: Az adat jellegének ismeretében sokkal jobb tömörítési ráták érhetőek el, mint a hagyományos algoritmusokkal.
- Példagenerálás: Új, az adatbázishoz hasonló mintaelemek generálása (a minta eloszlásának tanulása)
Klaszterezés
- Marketing, célzott reklám, ajánlórendszerek: hasonló ügyfelek csoportosítása célozott ajánlatokhoz.
- Klasszikus computer vision, pl. képszegmentálás
- Anomális (outlier) detektálás
Tömörtés / dimenziócsökkentés
- Bizonyos fajta adat jellegéhez illeszkedő tömörítés
- Kevesebb tárhely, sávszélesség használat.
- Tömörebb reprezentációval sokszor könnyebb dolgozni és könnyebb lehet megtalálni a hasonló elemeket.
- 2-3 dimenziós reprezentációban a mintaelemek elhelyezése még vizualizálható is.
A tömörítés / dimenzió redukció feladata jól definiált, azonban a hatékony tömörítés kihasználja, hogy a tömörített adatok hasonló jellegűek. Sok különböző fajta adat tömörítéséhez nehéz lenne egyedi algoritmusokat írni.
Feladat formális megadása
: Az input ? A tömörítést végző hipotézisfüggvény, pl. egy autoenkoder neuronháló.
költség: közelítse meg minél jobban -et (jó rekonstrukció)
Felügyeletlen tanulás alkalmazásai
- Zajcsökkentés
- Intelligens felskálázás
- Példagenerálás
- DeepFake
- Kódgenerálás
- Szöveggenerálás
Megerősítéses tanulás
Markov Döntési Folyamat (MDP)
- input-címke párok helyett állapot-akció párok.
- Az akciónk nagyban befolyásolja a következő állapotunkat.
- költség helyett jutalom (nem feltétlen azonnal)
- Cél: hosszútávon maximalizáljuk a jutalmak összegét

Példa: Automata autó
- - állapot: Az autó sebessége, az autó környezete
- - akció: Gázpedás, fékpedál, kormény forgása
- - jutalom:
- Eljutottunk a célhoz nagy jutalom
- Elütöttünk valakit nagy büntetés
- Nem tartottuk be a sebességhatárt kisebb büntetés
A mesterséges intelligencia főbb kérdései
- Általánosító képesség: A betanult modellünk memorizálja a tanító példákat egyenként, vagy valóban “hasznos” dolgokat tanul?

- Magyarázhatóság: A kritikus alkalmazásokban használt szoftvereket behatóan tesztelik,
formálisan verifikálják sokszor.
A deep learning módszerei csak tapasztalati úton tesztelhetők, nem tudjuk róluk megmondani, hogy “logikus módon” hozták-e a döntéseiket - Boztonság - adversarial attack: Akár a neuronháló architektúrája és paramétereinek
ismerete nélkül kereshető kismértékű speciális zaj, mellyel módosítva az
inputot, a becslés drasztikusan változik.

Szoftver
Python
- Magas szintű
- Automatikus memóriakezelés
- Futásidejű típushozzárendelés és ellenőrzés
- Interpretált nyelv
- Egyszerű szintaxis
- Hordozható
- Rengeteg eszköz, könyvtár
Szóval kényelmes és gyors fejlesztést tesz lehetővé, de lassú végrehajtás és futásidőben kiderülő hibák.
A számításigényes műveleteinket hatékony, más nyelven írt könyvtárak segítségével valósítjuk meg. A Python-t csak a szkriptelésükre használjuk!
NumPy
- Vektorizált programozás, vektorműveletek.
- A grafikus kártyák a vektorizált műveletekre optimalizáltak.
- A gépi tanulásban használt műveletek szinte mindig vektorizálhatóak.
- A vektorizált programozással írt kód általában sokkal tömörebb.
- Egy tömb elemének hivatkozása
- dimenziós tömbök
- Broadcasting
Keras
- Tensorflowra épülő magas szintű könyvtár neuronhálókhoz.
Google Colab
Források
Regressziós technikák
Regresszió
Regresszió: folytonos értékű címke (a címkehalmaz végtelen)
Példa: autók számának, vagy életkor becslése.
Lineáris regresszió
Hipotézisfüggvény: nagyon egyszerű (lineáris) hipotézisfüggvény:
a hipotézisfüggvény paramétere, ebben az esetben az egyenes meredeksége lesz.

Költségfüggvény
Hogyan állapítjuk meg mennyire jó a becslés?
A költségfüggvénnyel:
A költségfüggvény megadja, hogy mennyire tér el a valódi címke és a becslésünk adott paraméter értékek esetén.
Lineáris regresszió esetén a költségfüggvény:
Azaz, a hipotézisfüggvény által becsült címkék és az igazi címkék különbségének a négyzete, átlagolva a mintaelemek felett: MSE (Mean Squared Error, átlagos négyzetes eltérés).
A feladat tehát:
Keressük azt az optimális paramétert (), mellyel minimális a költség, azaz a címke predikciónk átlagos négyzetes eltérése az igazi címkétől.

Grádiens módszer
Honnan tudjuk, hogy merre kell lépnünk, hogy a költség csökkenjen?
Nézzük meg merre lejt leginkább a költségfüggvény az aktuális paraméterértékben állva!
Mi adja meg meredekségét egy adott pontban?
- a deriváltja a pontban.

Gradient descent: Iteratívan lépegetünk -val, abba az irányba, amerra a legnagyobb a lejtése a költségfüggvénynek az aktuális -ban.
repeat until convergence {
grad := J'(θ)
θ := θ - α * grad
}
: learning rate
Bias
Mi hiányzik?
Az eddigi modellünk túlzottan limitált. A hipotézisfüggvény egy olyan egyenes volt, amely az origón kellett, hogy átmenjen
A meredekség mellé egy konstans (bias / intercept) paramétert is bevezetünk.
Új hipotézis:

A költségfüggvény továbbra is MSE, de a hipotézis függvény megváltozott.
A költségfüggvény továbbra is kvadratikus. Mivel már két paraméterünk van, egy elliptikus paraboloid.

Hogyan válasszunk paramétereket, hogy a költség csökkenjen?
Használjuk a gradiens módszert: lépegessünk a legnagyobb meredekségű lejtés irányába.
Ezt az irányt egy adott pontban a gradiens vektor fogja megadni, melynek elemei a J költségfüggvény parciális deriváltjai az egyes paraméterek szerint.
A költségfüggvény parciális deriváltjai:
Grádiens módszer két paraméter esetén
repeat until convergence {
grad0 := J'{θ0}(θ0, θ1)
grad1 := J'{θ1}(θ0, θ1)
θ0 := θ0 - α * grad0
θ1 := θ1 - α * grad1
}
{}: szerinti parciális derivatív.
Garantált-e, hogy a gradiens módszerrel megtaláljuk a lineáris regresszió optimális megoldását?
- Megfelelően kicsi esetén igen.
Garantált-e, hogy a gradiens módszerrel megtaláljuk tetszőleges költségfüggvény globális minimumát?
- Nem. Eljuthatunk az egyik lokális minimum pontba, de amennyiben a költségfüggvény nem konvex, akkor nem garantált, hogy ez a globális minimum lesz.
Miért pont négyzetes hibát használunk költségként?
- Ha analitikusan szeretnénk megoldani, akkor ez egyszerűbb
- Mivel a költségfüggvény kvadratikus, ezért a deriváltja lineáris, így a lépésméret "magától" leskálázódik, ahogy közelebb érünk az optimumhoz.
Források
Többváltozós lineáris regresszió, klasszifikáció, logisztikus regresszió
Több input-változós lineáris regresszió
Hipotézisfüggvény változó esetén:
Vektoros alakban:
Költségfüggvény változó esetén:
Feature scaling
Az input változók azonos nagyságrenre hozása
- intervallumra min-max skálázás
- sztenderdizálás (ez preferált)
Klasszifikáció
Példa: kategorizáljuk a fényképeket a rajta szereplő állatok szerint.
Pl. "kutya" = 1, "macska" = 2, "papagáj" = 3
Ekkor a regresszióval ez a baj: macska = 0.5 * "kutya" + 0.5 * "papagáj"
Ehelyett valószínűséget fogunk becsülni
- Mennyi a valószínűsége, hogy egy mintaelem az adott kategóriába tartozik?
Bináris klasszifikáció
A becslés folytonos érték, és mivel valószínűséget becslünk, a címkék gyakorlatban folytonos értékek, így megpróbálkozhatunk lineáris regresszióval.
Sigmoid függvény
A lineáris regresszió nem ideális klasszifikációs feladatokhoz, mert nagyon érzékeny a kiugró értékekre.
Használhatunk inkébb sigmoid függvényt:
Logisztikus regresszió:
Logisztikus regresszió
Itt már a mean squared error költségfüggvény nem lesz konvex, ha a az új -et behelyettesítjük.
Itt inkább ezt használjuk (cross entropy):
Ezután használhatjuk a gradiens módszert.
Források
Python, numpy
Python alapok
- Tömor, magas szinten absztraktált
- Interpretált
- Dinamikus, erős típusrendszer
- Többparadigmás
- Open-source
- Párhuzamosítási lehetőségek korlátozottak
- Egyes feladatokhoz lassú lehet
Python objektumok
- Memóriacímük lekérhető az
id()függvénnyel - Vannak alaptípusok, konténertípusok és felhasználó által definiált típusok, lekerhető az
type()függvénnyel.- vannak mutable és immutable típusok
Iterálható konténertípusok
- Képesek egyesével visszaadni az elemeiket
- Így lehet rajtuk iterálni, pédául
forciklussal - A gyakorlatban ez azt jelenti, hogy értelmezhető rá az
__iter__()függvény, mely egy iterátor objektumot ad vissza - A
__next__()függvénnyel érjük el a következő elemet - Iterátort össze lehet gyűjteni szekvencia típussá
StopIterationexceptiont vált ki, ha elfogynak az iterálható elemek.
Adatszerkezetek
- Lista
- Elemei lehetnek különböző típusúak
- Dinamikus memóriafoglalás
- Tömbként van implementálva
- Több elem elérése:
List[from:to:step]
- Tuple
- Set
- Minden elem egyszer szerepelhet
- Vegyes típusok is lehetnek, de csak immutable típusok
- Dict
Függvények
- Opcionális paraméterek (default értékkel)
- Lambdák
Vezérlési szerkezetek
-
Kódblokkok indentációval vannak jelölve
-
Szülő utasítás után indentált blokk kell
-
Egy blokk ugyan annyi karakterrel van indentálva
-
Indentáció lehet tab, vagy space, de keverni nem lehet
-
if-elif-else -
for, while -
list comprehension
Hasznos függvények
map()filter()zip()enumerate()min(), max()any(), all()
Hibakezelés
- Szintaxis hibák: ha az interpreter nem tudja értelmezni a kódot
- Futási idejű
exception-ök assert-ekunittestmodul:assertTrue(), assertEqual()
Numpy
- Gyors numerikus számítások
- Hatékony nyelveket írt, párhuzamosító kódot hív meg.
- Optimálish cache használat
- Sok neurális háló könyvtár épül numpy-ra
ndarray
- Homogén típusú elemeket tartalmaz, 0-tól indexelve
- Meghatározó attribútumok:
shape, dtype - Az elemek száma nem változhat, de az alakja igen
- A memóriában folytonosan, egy dimenzióban helyezkednek el az adatok
Univerzális függvények
- Elemenkénti műveleteket hajtanak végre
ndarray-eken - Egyszerű algebrai függvények
- A broadcasting megengedi, hogy a műveleteket olyan tömbökön is végrehajtjuk, amelyeknek nem egyezik meg teljesen az alakjuk
Broadcasting
- Ha két tömb dimenziójának száma nem egyezik, a kevesebb dimenzióval rendelkező tömb új első tengelyeket kap. Éppen annyit, hogy dimenzióik száma egyezzen.
- A második szabály, ha valamelyik tengely mentén az egyik tömb hossza egy, az a tömb azon a tengly mentén annyiszor ismétlődik, hogy a hossza egenlő legyen a másik tömbével.
Advanced indexing
- Advanced index esetén slice-ok helyett használhatunk bármilyen szekvenciát, ami integereket vagy logikai változókat tartalmaz
- Mindig másolatot ad vissza az egyszerű indexeléssel szemben
- Állhat advanced indexelt tömb értékadás bal oldalán, ilyenkor nem készül másolat, és az eredeti tömb íródik felül.
Hasznos függvények
- Szélsőértékek:
np.max(), np.min()np.argmax(), np.argmin()
- Aretmetikai műveletek
np.sum(), np.cumsum()np.prod(), np.cumprod()np.mean(), np.var(), np.std()
- Logikai műveletek
np.all()np.any()
ndarray.flatten()np.concatenate()np.stack()np.linspace(), np.logspace()np.unique()np.bincount()np.diff()
Források
Feladatmegoldások
Jövő órán röpdolgozat a pythonos órák anyagából.
Források
Betanítási költség, túltanulás, alultanulás, neuron
Lineáris regresszió
- A lineáris regresszió jól működik olyan mintán, ahol a változók lineáris kombinációja jól közrlíti a mintát.
- Mit tehetünk, ha ez nem áll fenn?
- Pl.: Polinómiális regresszió (a mintákat hatványozzuk, amit keresünk, azok az együtthatók)
- Lineáris regresszióként megoldhatjuk, ha behelyettesítjük az előre kiszámolt változók hatványokat.
- Az új változókra alkalmazhatunk feature-scaling-et, hogy csökkentsük a hatványozás okozta nagyságrendi problémákat.
A minta felosztása
Modell életciklusa:
- training set
- test set
- validation set
A költség alakulása a betanítás során
Alultanulás:
- Pl. ha polinomiális regresszió során túl alacsony fokú polinomot használunk, vagy kicsi, vagy "fura" a training set
- A teszt hiba (és a training is) nagy.
Túltanulás
- Pl. Ha túl kicsi a training set, és specializálódik a model erre a training set-re
- A training set hiba javul, de a teszt set-en nem változik, vagy nő
- Így a model nem lesz elég generikus
Alultanulás és túltanulás elkerülése
- Alultanulás: A modell komplexitása túl kicsi, bonnyolultabb modell szükséges.
- Túltanulás:
- A modell elég összetett ahhoz, hogy pontosan a tanítóhalmaz egyes elemeinek sajátosságaira fixál rá.
- A modell komplexitását is csökkenthetjük, de ez nem kívánatos.
- (L2) Regularizáció: hatalmas együtthatók csökkentése: a költségfüggvény büntesse a nagy együtthatókat (azoknak a négyzetüket).
- Early stopping: Amikor a teszt halmazon mért költség elkezd nőni, akkor megálunk.
- Ilyenkor a teszthalmazt is belevontuk a tanulásban (big no-no)
- Ilyenkor használunk egy validációs halmazt is, amit a teszt halmaz helyett vonunk be.
- A validációs halmazzal optimalizáljuk a "hiperparamétereket"
Betanítás folyamata
- hiperparaméterek konfigurációja
- paraméterek optimalizálása, hiperparaméterek megváltoztatása
- teszt futtatása, hibamérés
Neuron
- Bemenetek kimenetek (konstans jel)
- A bemenetekből egy lépcsőfüggvényel kapjuk meg a konstans kimenetet
- Együttható
- Bias
- Aktivációs függvény
- pl. sigmoid
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
8. Előadás
Multilayer perceptron
- Az előző előadáson leírt neuronokat rétegekbe rendezzük, így egy komplexebb modell hozva létre.
- : súlymátrixok és bias vektorok halmaza.
- ahol a rétegben található neuronok száma.
Kétrétegű neuronháló hipotézisfüggvénye
- Költségfüggvények egyelőre maradnak.
- Klasszifikáció: logistic loss
- Regresszió: MSE
- A és aktivációs függvények fontosak, mert nemlinearitást adnak a hipotézisfüggvényhez, amely lehetővé teszi a tanulást. (különben nem nől a kifelyező erő, csak bonyolultabb lineáris regressziót kapunk)
Aktivációs függvények
- sigmoid
- tanh
- ReLU
Mit tanul egy neuronháló?
- Mit tanul egyetlen neuron?
- Egyetlen lineáris döntési felületet (hiszen logisztikus regresszióról van szó)
- A neuronháló ezen lineáris döntési felületek valamilyen kombinációját tanulja
Multiclass
- Ebben az esetben az nem egy skalár, hanem egy vektor.
- Multiclass klasszifikációnál használjuk a softmax függvényt az utolsó rétegen
Források
9. Előadás
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
Túltanulás elkerülése, konvolúciós hálózatok
Túltanulás elkerülése
- adat auhmentáció
- Képek: eltolás, forgatás, tükrözés, zaj, torzítás
- Hang: nyújtás, frekvencia változatatás, zaj
- dropout: nem minden neuron vesz részt mindig egyszerre a tanulásban
Konvolúciós neurális hálózat
Források
12. Előadás - nincs jegyzet
Szoftvertechnológia (F) előadás
Alapadatok
Idő: Kedd, 8:00 - 10:00
Helyszín: Déli Tömb 0-821 Bólyai János terem
Oktató: Szendrei Rudolf, https://swap.web.elte.hu/
Csoport: 90
Értékelés
- Félévvégi teszt
- Gyakorlati projekt
Források
Szoftverfejlesztési folyamat
- Szoftverfejlesztési folyamat
Szoftverfejlesztés
A szoftverek nélülözhetetlen alkotóelemei a modern világnak.
- Szémos célt szolgálnak
- Különböző felépítésűek
- emiatt megvalósításuk módja jelentősen eltérhet
A szoftverekben jelentős része hibás, a szoftverfejlesztési munkák jelentős része kudarcba fullad, ennek okai:
- Egyre nagyobb számban, egyre összetettebb szoftverekre van szükség
- Alacsonyabbak az elvárások a szoftverekkel szemben.
Emiatt nagy szükség van professzionális szoftverfejlesztésre
A szoftvertechnológia
Egy szoftvernek, mint terméknek gyártási technológiára van szüksége, amely garantálja a program funkcióit, minőségét, költségét és határidejét.
A szoftvertechnológia feladata szoftverek rendszerezett, felügyelt, minősített fejlesztése, működtetése és karbantartása
- programok
- dokumentáció
- konfiguráció
- adatok
A szoftverek többsége nagy méretű, nagy bonyolultságú programrendszer, amely
- Rendszerint csapatmunkában készül
- Hosszú élettartamú, karbantartást és bővítést igényel
Minőségi mutatók
A szoftvereknek megfelelő színvonalon kell biztosítania az elvárt funkciókat, amit a szoftver minőségi mutatóival (quality characteristics) írhatunk le
- Karbantarthatóság
- Megbízhatóság és biztonság
- Hatékonyság
- Használhatóság, hozzáférhetőség
Szoftvertechnológiai projekt
A szoftver fejlesztésének folyamatát projektnek, előállításának felügyeletét projektmenedzselésnek nevezzük.
A projektért felelős személy a projektmenedzser (project manager), aki
- Biztosítja, hogy a szoftver megfelel az előírt minőségnek, és elkészül a megadott határidőre a költségkereten belül.
- Szervezi, irányítja, ütemezi a projektben részt vevő csapat munkáját, és biztosítja a szükséges hardver és szoftver erőforrásokat.
- Garantálja a módszerek és szabványok alkalmazását
- Gondoskodik a projekt dokumentáltságáról
A szoftverfejlesztési csapatnak számos további tagja lehet, akik különböző szerepeket töltenek be, pl.:
- Termékgazda: üzleti folyamatok, prioritások és elfogadási feltételek kezelése
- Programgazda: fejlesztés ütemezése, feladatok elosztása és követése.
- Tervező: szoftver magas szintű tervének elkészítése, technikai döntések kezelése
- Fejlesztő: szoftver implementációja
- Minőségbiztosítás: tesztelés tervezése, megvalósításai

A szoftver életciklus
Minden szoftver rendelkezik életciklussal, amely meghatározza létét a feladat kitűzésétől a program használatának befejezéséig.
Az életciklus általában négy fő fázisra bontható:
- specifikáció
- tervezés és implementáció
- verifikáció és validáció
- evolúció

Specifikáció
A specifikáció (software specification) célja a feladatot megoldó szoftver funkcióinak tisztázása, a rendszerre és a fejlesztésre vonatkozó elvárások megadása.
feltérképezi a követelményeket felhasználói, valamint fejlesztői szemszögből, lépései:
- megvalósíthatósági elemzés
- követelmény feltárás és elemzés
- követelmény specifikáció
- követelmény validáció
Eredménye a szoftver követelmény-leírása (software requirements specification)
Tervezés és implementáció
A szoftver tervezése és implementációja (software design and implementation) feladata a specifikáció átalakítása egy végrehajtható rendszerré.
Meghatározza a rendszer szerkezetét (felépülés), felületét (be- és kimenet), működését (alkalmazott algoritmusok, kommunikációs folyamatok)
A folyamat során elkészül a szoftver rendszerterve (software design description), amely tartalmazza a program statikus és dinamikus szerkezetét, a kommunikációs csatornák feltérképezését, az implementációs és tesztelési tervet.
Elkészíthető a szoftver prototípusa (prototype), amely a program egyszerűsített megvalósítását tartalmazza.
Az implementációhoz megfelelő szoftverfejlesztési környezetet kell használnunk, a programkód változásait verziókövetéssel tartjuk nyilván.
Az implementáció részeként az egyes programegységek tesztelése is megtörténhet.
A szoftverek tervezésének és programozásának módszerét nevezzük programozási paradigmának.
- Meghatározza a programozási stílust, az absztrakciós szintet.
- Meghatározza az alkalmazható programozási nyelvek körét is, és fordítva.

Validáció és evolúció
A verifikáció és validáció (software verification and validation) célja megmutatni, hogy a rendszer megfelel a specifikációnak, valamint a felhasználói elvárásoknak.
Az evolúció (software evolution) során új követelményeknek megfelelően bővítjük a szoftvert, illetve korrigáljuk a felmerülő hibákat.
További lépések is kísérhetik a fejlesztési folyamatot, pl.
- kihelyezés (deployment): a program üzembe állítása, és elérhetővé tétele.
- tréning és támogatás (training and support): a felhasználókkal való kapcsolattartás (annak biztosítása, hogy a szoftvert megfelelően tudják kezelni és használni)
A szoftver dokumentációja két részből tevődik össze:
- felhasználói dokumentáció, amely tartalmazza a szoftver üzembe helyezésének, funkcióinak bemutatását
- fejlesztői dokumentáció, amely tartalmazza a szoftver megvalósítását folyamatát és részletes ismertetését
Ütemterv
A szoftver életciklus fázisai (feladatai) további fázisokra (részfeladatokra) tagolhatóak, így egy hierarchikus feladatszerkezetet kapunk.
- Az egyes feladatokra erőforrásokat és időkorlátot adhatunk
- Az egyes feladatok között függőségeket állapíthatunk meg
- Ezek alapjén elkészíthetjük a projekt ütemtervét
- Tartalmazza a feladatok időbeli beosztását, függőségeit, felelőseit, így áttekinthetővé teheti az erőforrás szükségleteket.
- Általában a specifikáció során készül el, de később módosulhat.
Mérföldkövek
A feladatokhoz mérföldköveket (milestone) rendelhetünk, amelyek lehetőséget adnak a projekt haladásában történő betekintésre.
- A márföldkő egy adott cél adott időpontra történő elérését jelenti, így névvel, eseménnyel, céllal rendelkezik.
- A mérföldkövek be nem tartása általában korrekciókat követel a projekt lefutásában.
- Kellően konkrétnak, ellenőrizhetőnek, számonkérhetőnek kell lennie.
- A fő mérföldkövek az egyes fázisok lezárását jelentik, ezen kívül számos további mérföldkő adható.
Az UML
A szoftverfejlesztési életciklust folyamatosan követi a modellezés, ennek eszköze az egységes modellezési nyelv (Unified Modeling Language, UML), amely egy öt pillérű szemléletrendszerrel rendelkezik:
- Használati: a szoftver szolgáltatásai és azok kapcsolata a felhasználókkal.
- Szerkezeti (statikus): a rendzser és a programegységek felépítése, kapcsolatai.
- Dinamikus: a programegységek viselkedése.
- Implementációs: a megvalósítás szempontjai, komponensei.
- Környezeti: hardver és szoftver erőforrások.
Szoftvereszközök
A fejlesztőcsapat munkáját megfelelő szoftvereszközökkel kell alátámasztani
- Projektirányítási eszközzel (project tracking system), amely támogatja a dokumentálást és a feladatok követését.
- Fejlett tervezőeszközzel (case tool), ahol a fejlesztés folyamata és a felelősség is nyomon követhető.
- Integrált fejlesztőkörnyezettel (IDE), amely elősegíti a csapatmunkát.
- Verziókövető rendszerrel (revision control system), amely lehetővé teszi a programkód változásainak követését.
- Folyamatos integrációs eszközzel (continuous integration), amely elősegíti a tevékenységek automatizálását.
A vízesés modell
A szoftverfejlesztési modell határozza meg az életciklus egyes fázisai közötti kapcsolatot, időbeliséget.
A legegyszerűbb fejlesztési modell a vízesés (waterfall) modell, amelyben az egyes fázisok lineárisan követik egymást.
- Előre megtervezi a projekt időtartamát, ráfordításait.
- Elvárja minden fázis megfelelő dokumentálását, amely tartalmazza annak eredményeit.
- Előnyei: jól strukturált, dokumentált folyamatot biztosít.
- Hátrányai: nem teszi lehetővé a követelmények megváltoztatását, nem készül fel az esetleges nehézségekre (nincs kockázatkezelés).

Prototípusok
A szoftverfejlesztés során felmerülő nehézségek könnyebben előreláthatóak, ha a szoftvernek elkészítjük a prototípusait (prototyping), amely lehet:
- Horizontális prototípus: interakciós szempontból mutatja be a szoftvert.
- Vertikális prototípus: egy adott funkciócsoport részletes megvalósítása.
A folyamat során megvalósított prototípusok a szoftver részévé válhatnak (evolutionary prototyping), vagy szolgálhatják csak a bemutatást/ellenőrzést, és ténylegesen nem kerülnek felhasználásra (throwaway prototyping).
A spirális modell
A (Boehm-féle) spirális modell egy kockázatvezérelt fejlesztési modell, amelyben a folyamat során elsőként prototípusok kerülnek megvalósításra, amelyek kiértékelése után kerül megvalósításra a tényleges szoftver.
- A fejlesztés ciklusokban történik, amelyben az elkészített prototípusok, valamint a továbbfejlesztésével kapcsolatos kockázatok kiértékelésre kerülnek.
- Előnyei: jobban alkalmazkodik a változó követelményekhez, a prototípusok lehetővé teszik a nehézségek előrelátását.
- Hátrányai: költségesebb a prototípus elkészítése és a kockázatkiértékelés végett, továbbá a prototípusok megzavarhatják a felhasználót.

Az inkrementális modell
Az inkrementális modell több lépésből építi fel a folyamatot, és több változatban állítja elő a szoftvert.
- Minden változat egy újabb funkcionalitással bővíti a szoftvert, a fázisok rövidek, gyors visszajelzésekkel.
- Az egyes fázisok átfedésben vannak, és kihatnak egymásra.
- Előnyei: gyorsan alkalmazkodik a változó követelményekhez, a felhasználó jobban követheti a fejlesztési folyamatot.
- Hátrányai: kevésbé menedzselhető, tervezhető, áttekinthető, nehezebben validálható.

Agilis szoftverfejlesztés
Az agilis szoftverfejlesztés célja a gyors alkalmazásfejlesztés megvalósítása, inkrementális alapon.
- A szoftver folyamatos fejlesztés és kiadás alatt áll (continuous delivery), a sebesség állandó, a változtatások minden lépésben beépíthetőek (welcome changes).
- A működő szoftver az előrehaladás mérőeszköze, előtérben az egyszerűség, ugyanakkor folyamatos odafigyelés a megfelelő tervezésre, optimalizációra.
- A fejlesztést általában önszervező, kis csapatok végzik, megosztott felelősséggel, folytonos interakcióval, gyors visszajelzésekkel.
- Előnyei: jól alkalmazkodik a változtatásokhoz, hatékonyabbá teszi a fejlesztési folyamatot.
- Hátrányai: egyes tényezői nehezen megvalósíthatóak, különösen nagyobb szoftverek esetén a megvalósításhoz képzett fejlesztők kellenek, a dokumentáció hiánya megnehezíti a későbbi evolúciót.
Az agilis Kiáltvány
Azzal leplezzük le a szoftverfejlesztés jobb módjait, hogy csináljuk és segítünk másoknak is csinálni. Ezen a munkán keresztül következő értékekhez jutottunk el:
- Egyének és kölcsönhatások előnyben részesítése a folyamatok- és eszközökkel szemben.
- Működő szoftver előnyben részesítése az átfogó dokumentációval szemben.
- Ügyféllel való együttműködés előnyben részesítése a szerződéses megállapodással szemben.
- Változásokra adandó válasz előnyben részesítése egy terv követésével szemben.
Habár a jobb oldali elemekben is van érték, mi sokkal értékesebbnek tartjuk a baloldali elemeket.
Scrum módszer
Az agilis fejlesztés menedzselését az egyes változatok előállítása szempontjából közelítik meg, amelyhez a Scrum módszer ad egy általános modellt.
- Architekturális tervezés, amely megadja a szoftver magas szintű vázát.
- Futamok (sprint), amelyek az egyes változatokat állítják elő, és rögzített hosszúságúak (2-4 hét).
- Projektzárás, a szükséges dokumentáció előállítása.
Nincs projektmenedzser, de minden futamnak van felelőse (scrum master), akinek a személye futamonként változik.
Minden futam egy összetett folyamat megtervezett lépésekkel
- Feladatok felmérése (select), lefejlesztése (develop), áttekintése (review), kiértékelése (assess).
- A megvalósítandó funkciók a termékgazdával egyetértésben kerülnek kiválasztásra a teendők listájából (product backlog).
- Naponta rövidebb megbeszélések (stand-up meeting) a teljes csapat számára.
- Ciklus elején/végén hosszabb megbeszélések (sprint planning, sprint review), valamint visszatekintés (retrospective) a termékgazdával.

Csoportosítás
A szoftverfejlesztési modelleket 3 csoportba soroljuk.
- Terv-vezérelt (plan-driven): célja a rend fenntartása, a szoftver fejlesztése előzetes specifikáció és tervezés alapján történik, igyekszik garantálni a minőséget.
- Agilis: célja a változáshoz történő alkalmazkodás, az egyszerűség, így kevésbé garantálja a minőséget.
- Formális: garantálja a minőséget, az implementáció bizonyíthatóan helyes megoldását adja a specifikációnak.
A gyakorlatban a fejlesztőcsapat és a feladat befolyásolja leginkább a választott módszert, sokszor különböző módszerek vegyítve jelennek meg.
Források
Specifikáció és követelménymenedzsment
A specifikáció
A specifikáció célja a eladatot megoldó szoftver funkcióinak tisztázása, a rendszerre és a fejlesztésre vonatkozó elvárások megadása.
- Feltérképezi a követelményeket felhasználói, valamint fejlesztői szemszögből, lépései:
- megvalósíthatósági elemzés
- követelmény megállapítás és elemzés
- követelmény specifikáció
- követelmény validáció
- Eredménye a szoftver követelmény-leírása.

Megvalósíthatósági elemzés
A megvalósíthatósági elemzés (feasibility study) azt vizsgálja, hogy a szoftver megvalósítható-e, és üzletileg megtérül-e a befektetés, ezen belül:
- Milyen erőforrások szükségesek, és ezek rendelkezésre állnak-e
- Mi a megvalósítás költsége, időtartama
- A fejlesztést követően a szoftver igényel-e üzemeltetést, karbantartást, és ez milyen költségeket jelent
Az elemzést gyorsan, alacsony költségek mellett kell elvégezni.
Amennyiben a fejlesztett szoftver egyedi, az elemzést ajánlattétel követi a vevők számára.
Követelmény feltárás és elemzés
A követelmények feltárása és elemzése (requirements elicitation and analysis) során követelményeket állapítunk meg, három lépésben:
- Kutatás: meglévő rendszerek, egyeztetés, interjúk a lehetséges felhasználókkal, kezdeti követelmények meghatározása.
- Osztályozás: a követelmények rendezése, csoportosítása, alrendszerekhez történő besorolás.
- Prioritizálás: fontossági sorrend felállítása, ütközések feloldása, szükségtelen, vagy megvalósíthatatlan követelmények elhagyása.
Követelmények feltárása
A követelmények feltárását és leírását számos tényező nehezítheti.
- A vevők bizonytalanok az elvárásokban
- A vevők nem egyértelműen fejtik ki az elvárásokat.
- A vevők nem rendelkeznek informatikai ismeretekkel.
- A vevők nem közvrtlenül a szoftver felhasználói, így a felhasználói igények eltérhetnek.
- A körülmények változhatnak a specifikáció során
A követelmények alapján létrehozhatóak a rendszer modelljei, prototípusai, pl.:
- Felhasználói felület terve, menürendszer
- Egyszerűsített vizuális megjelenés, animáció
Követelmények típusai
- Funkcionális:: a szoftver által nyújtott szolgáltatások, reakciók, viselkedések leírása
- Nem funkcionális: megszorítások a szolgáltatásokra, a
viselkedésre
- Termék követelmények: hatékonyság (teljesítmény, méret), megbízhatóság, biztonság, hordozhatóság, felhasználhatóság.
- Menedzselési követelmények: környezeti, működési, fejlesztési.
- Külső követelmények.
Termék Követelmények
- Hatékonyság: a szoftver által a hardver erőforrásokra (processzor, memória, merevlemez, sávszélesség) való támaszkodás mértéke, amelyet a lehető legkisebbre kell szabni.
- Megbízhatóság: a szoftver által biztosított funkcionalitás garantálása (correctness) a környezetben bekövetkezett változások ellenére, abban az esetben is, amennyiben azok nem felelnek meg a specifikációban elvárt követelményeknek (robustness)
- Biztonság: a szoftverben által tárolt adatok védelmének mértéke az illetéktelen hozzáféréssel szemben.
- Hordozhatóság: szoftver kompatibilitásának mértéke különböző hardver és szoftver platformokkal, valamint az azokra történő átvitel könnyedségének mértéke.
- Felhasználhatóság: a szoftver (használatának, telepítésének, üzemelésének) elsajátításának könnyedsége a különböző képzettségű és hátterű felhasználók számára; akadálymentesség.
Menedzselési követelmények
- Környezeti:
- a rendszer által igényelt hardver erőforrások
- a rendszer használatához szükséges további szoftverek, amelyekkel együttműködik.
- Működési:
- a felhasználás paraméterei (gyakoriság, időtartam, felhasználók száma, rendelkezésre állás mértéke)
- a felhasználók jellege (szaktudás, informatikai ismeretek)
- Fejlesztési:
- a fejlesztés módszertana, programozási paradigmái, szükséges eszköztára.
- a felhasznált programozási nyelvek és könyvtárak.
Külső követelmények
- Jogszabályoknak való megfelelés
- Etikai kérdések a felhasználó adataival, és azok továbbadásával szemben.
- Tulajdonjogi kérdések a begyűjtött adatokkal, az esetleges külső fejlesztésekkel kapcsolatban.
Követelmény specifikáció
A követelmény specifikáció (requirements specification) az elemzés során kapott információt alakítjuk át egységes alakba.
A felhasználói szinten csak alapjaiban, a fejlesztői szinten részletesen megadjuk.
A leírás történhet:
- Beszélt nyelven
- Formalizált leírással
- Formális matematikai leírással
- Formális leírónyelvek segítségével
- Metrikák segítségével
Használati esetek
A használati esetek (use case) diagramja azt ábrázolja, miként működik együtt a felhasználó a rendszerrel.
Szabványos módja a funkcionális követelmények leírásának.
A diagram elemei:
- Aktor: a felhasználó, aki a rendszert használja
- Funkció: a rendszer egy szolgáltatása, viselkedési mintája
- Reláció: kapcsolat a funkció és az aktorok között

A relációk típusai:
- Használat: az aktor igénybe veszi a rendszer egy funkcióját. (csak aktor és funkció között)
- Általánosítás: egyik funkció, vagy aktor egy bővebb halmaz, mint a másik.
- Tartalmazás: egyik funkció részét képzi egy másik funkciónak.
- Kiterjesztés: egyik funkció kiterjesztése egy másik funkcióval.
- Előfeltétel: egy funkciónak meg kell előznie egy másik funkciót
- Rákövetkezés: egy funkciót követ egy másik

Felhasználói történetek
A funkciók részletesebb kifejtését teszik lehetővé a felhasználói történetek.
A felhasználók által végzett tevékenységsorozatokat és azok lehetséges kimeneteleit adják meg különböző szituációkban.
A történetben azonosítunk egy szerepkört (user role) és egy célt, valamint megindokoljuk a cél szükségesség.
Egy történetre egy, vagy több esetet írhatunk fel, amelyben adott környezetben (given) egy tevékenységet végzünk (when), és erre valamilyen hatást (then) várunk.
Az eseteket úgy kell megfogalmaznunk, hogy az összes körülményt és lehetséges bemenetet figyelembe vesszük.
- Különös tekintettel a hibalehetőségekre (pl. hibás bevitel)
- Az egyes történetek egyúttal megadják a végleges alkalmazás funkcionális teszteseteit.

Követelmény validáció
A követelmények validációja (requirements validation) ellenőrzi a megadott specifikáció valószerűségét, konzisztenciáját és teljességét.
Mivel a követelményeknek ellenőrizhetőnek kell lennie, alkalmasnak kell lennie tesztesetek előállítására.
A validáció eredményezhet:
- Prototípust, amelynek célja a követelmények teljesíthetőségének rövid távú ellenőrzése.
- Teszteseteket, amelyek a végleges alkalmazáson ellenőrzik a követelmények teljesülését elsősorban a funkcionális követelményekre.
Követelmény-leírás
A követelmény-leírás tartalmazza a szoftver
- Célját, helyét, szükségességét, előzményeit, előnyeit
- A funkcionális és nem funkcionális követelmények leírását felhasználói és fejlesztői szemszögből.
- A rendszer átfogó architektúráját és modelljeit
- Áttekintést az implementáció és az evolúció számára
- Fogalomjegyzéket
A követelmény-leírás felépítése:
- előszó (célközönség, dokumentum-történet)
- bevezetés (szoftver célja, helye, szükségessége, előnyei)
- fogalomtár (technikai áttekintés)
- követelmények felhasználói leírása
- rendszer architektúra (magas szintű áttekintés)
- követelmények fejlesztői leírása
- rendszer modellek (pl. felület terv, adatformátum leírás)
- rendszer evolúció (várható fejlesztések, karbantartás)
- függelék (pl. adatbázis terv, becsült hardver szükségletek)
- tárgymutató
Források
Objektumorientált tervezés
Objektumok, osztályok
Az objektumorientált tervezés során a rendszert az objektumok mentén építjük fel, ahol az objektum
- valóság absztrakcióját adja
- biztosít egy elvárt funkcionalitást
- adat es működés egymásba burkolásából épül fel
Egy adott feladatban az objektumokat be kell azonosítnaunk azáltal, hogy
- milyen funkciókat azonsítottunk az elemzés során, és azok milyen adatokkal dolgoznak
- a valóságban milyen építőelemeket tudnánk megfeleltetni a funkcióknak
A tervezés fázisai
A tervezés általában több fázisból épül fel, amely során finomítunk a terven, mivel meglehetősen nehézkes már az első fázis alapján beazonosítani a szükséges objektumokat, és azok felépítését.
Ezért, minden fázisban
- bevezethetünk új osztályokat a beazonosított feladatokra
- tovább pontosíthatjuk a már létező osztályok felépítését, az implementációs megkötéseket
- felbonthatunk osztályokat, amennyiben túl bonyolulttá, túl szerteágazóvá válnak
- összevonhatunk osztályokat, amennyiben túlzottan elaprózódnak
A tervezés alapelvei (SOLID)
- Single responsibility principle
- Open/Closed principle: a programegységek nyitottak a kiterjeztésre, de zártak a nódosításra
- Liskov substitution principle: az objektumok helyettesíthetőek altípusaik példányával
- Interface segregation principle: egy általános interfész helyett több kliens specifikus interfész
- Dependency inversion principle: az absztrakciótól függünk, nem a konkretizációtól
Az architektúra
Szoftver architektúrának nevezzük a szoftver fejlesztése során meghozott elsőfleges tervezési döntések halmazát.
Ezek erősen kihatnak a rendszer felépítésére, viselkedésére, és megváltoztatásuk később nehézkes.
A fő feladata a rendszer magas szintű működésének meghatározása, a komponensek és relációk kiépítése.
Minták a tervezésben
A monolitikus architektúra
A legegyszerűbb felépítést adja.
- nincsenek programegységekbe szétválasztva a funkciók
- a felületet megjelenítő kód vegyül az adatkezeléssel, a tevékenységek végrehajtásával
A modell/nézet architektúra
Különválasztja a felhasználói felülettel kapcsolatos részeket a ténylegesen a feladat megoldását szolgáló funkcionalitástól.
- a modell tartalmazza a feladat végrehajtását szolgáló programegységet (üzleti logikát)
- a nézet tartalmazza a grafikus felhasználói felület megvalósítását,a felület elemeit és az eseménykezelőket
- a nézet ismerheti a modell interfészét, és hívhatja annak publikus műveleteit
- a modellnek semmilyen tudomása nincs a nézetről, csak eseményeken keresztül kommunikálhat vele
Csomagdiagram
Célja a rendszer felépítése a logikai szerkezet mentén, azaz az egyes csomagok azonosítása és a beléjük tartozó osztályok bemutatása.
A csomagok között is létrehozhatunk kapcsolatokat (függőség, asszociáció, általánosítás, megvalósítás).
Továbbiak:
use: a csomag felhasznál egy másikatnesting: a csomag egy másiknak a részeimport: a csomag betölti a másikatmerge: a csomag tartalmazza, és kibővíti a másik teljes funkcionalitását.
A szoftverrendszer
Szoftver: programok + dokumentáció + konfiguráció + adatok
- mivel a megoldandó feladatok összetettek lehetnek, a megoldást lehet csak több program tudja megadni
- végrehajtás során ezek egymással kommunikálnak
Az egymással kommunikáló programok rendszerét szoftverrendszernek nevezzük. Ezek részeit komponenseknek.
Komponensek
Adott funkcionalitásért felel és fizikailag elkülönül.
- önállóan felhasználható, telepíthető
- a belső működése rejtett, a kapcsolatot interfészek bisztosítják
- szolgáltathat ilyan funkcionalitást, amelyet más komponensek használnak fel
- felhasználhat más komponenseket is
Komponensek például
- asztali alkalmazás
- mobil alkalmazás
- weblap
- adatbázis
Feloszthatjuk így is:
- végrehajtható állományok
- könyvtárak
Komponensdiagram
Ismerteti a rendszer komponenseit, az interfészeket és a köztük fennálló kapcsolatokat (connector)
Telepítési diagram
A szoftverrendszert kihelyezési és környezeti szempontból ábrázolja.
Ismeri azon csomópontokat (node), amelyeken az egyes alkotóelemei (artifact) találhatóak.
A rendszer alkotóeleme lehet bármilyen, fizikailag elkülönülő tartozéka a szoftvernek.
A rendszer egy csomópontja lehet egy hardware eszköz, és egy végrehajtási felület, amely biztosítja a szoftverek futását.
Adatformátumok
Minden, a szoftver számára bemenetként, vagy kimenetként szolgáló adat formátumát, felépítését meg kell adnunk.
Összetett adatok esetén támaszkodhatunk létező formátumokra:
- CSV
- XML
- JSON
A rendszerterv
A tervezés eredménye a szoftver rendszerterve, amely tartalmazza:
- a program statikus szerkezetét
- a program dinamikus szerkezetét
- a tárolt, kezelt, és eredményül adott adatok formáját
- a programok belső és külső interfészeinek leírását
- ajánlásokat az implementáció számára
A rendszerterv felépítése:
- előszó (célközönség, dokumentum-történet)
- bevezetés (szoftver célja, helye, szükségessége )
- fogalomtár
- rendszer architektúra (csomag-, komponens-, állapotdiagram)
- adattervezés
- rendszertervezés (statikus terv, dinamikus terv, interfész leírás, algoritmusok)
- felhasználói felület
- implementációs ajánlások
- függelék (pl.: adatbázis terv, becsült hardware szükségletek)
- tárgymutató
Források
Objektumorientált tervezési szempontok és minták
- Objektumorientált tervezési szempontok és minták
A tervezés alapelvei (SOLID)
- Single responsibility principle
- Open/Closed principle: a programegységek nyitottak a kiterjeztésre, de zártak a nódosításra
- Liskov substitution principle: az objektumok helyettesíthetőek altípusaik példányával
- Interface segregation principle: egy általános interfész helyett több kliens specifikus interfész
- Dependency inversion principle: az absztrakciótól függünk, nem a konkretizációtól
A tervezés során mintákra hagyatkozunk, a szoftver teljes architektúráját definiáló mintákat nevezzük architektúrális mintáknak (architectural pattern), az architektúra alkalmazásának módját, az egyes komponensek összekapcsolását segítik elő a tervminták (design pattern)
Single responsibility principle
Számos, jól megkülönböztethető felelősségi kör található az alkalmazásokban:
- perzisztencia, üzleti logika, vizualizáció, felhasználói interakció.
- adatformázás, konverzió, validáció
Elősegíti a programegységek közötti laza csatolást, viszont túlzott használata feltöredezheti a programszerkezetet
Open/closed principle
A programegységek nyitottak a kiterjesztésre, de zártak a módosításra.
- A programszerkezetet úgy kell megvalósítanunk, hogy új funkcionalitás bevezetése ne a jelenlegi programegységek átírását igényelje, sokkal inkább újabb programegységek hozzáadását.
A SRP és az OCP kiegészítik egymást, mivel az új funkcionalitás egy új felelősség bevezetését jelenti, így általában egyszerre szegjük meg a két elvet.
Liskov substitution principle
Bármely típus (osztály) példánya helyettesíthető altípusának egy példányával úgy, hogy közben a program tulajdonságai (funkcionális és nem funkcionális követelményei) nem változnak.
Megszorításokat tesz a szignatúrára
- elvárja a paraméterek kontravarianciáját, a visszatérési értékek kovarianciáját
- tiltja a kivételek típusának bővítését
Megszorításokat tesz a viselkedésre
- elvárja az invariánsok megtartását
- tiltja az előfeltételek erősítését, az utófeltételek gyengítését.
Interface segregation principle
Egy kliensnek sem szabad olyan interfésztől függenie, amelynek műveleteit nem használja.
Ezért az összetett interfészeket célszerű több, kliens specifikus interfészre felbontani, így azok csak a szükséges műveleteiket érhetik el.
Dependency inversion principle
Magasabb szintű programegységek nem függhetnek alacsonyabb szintű programegységtől, hanem mindkettőnek az absztrakciótól kell függenie.
Az absztrakció nem függhet a részletektől, a részletek függenek az absztrakciótól.
A megvalósítása számára a következőket jelenti:
- az osztály mezői a konkrét osztályok helyett az absztrakció példányát tartalmazzák
- a konkrét osztályok az absztrakció segítségével lépnek kapcsolatba egymással, a konkrét osztályok szükség esetén átalakíthatóak
- szigorú esetben konkrét osztályokból nem örökölhetünk, és már megvalósított metódust nem definiálunk felül
- az osztályok példányosítását egy külső programegység végzi, pl. függőség befecskendezés, gyártó művelet, vagy absztrakt gyártó segítségével.
Tervezési minták
Dependency injection
A végrehajtás során egy réteg (kliens) által használt réteg (szolgáltatás) egy, az adott körülmények függvényében alkalmazható megvalósítása kerül alkalmazásra.
Erről általában nem dönthet sem a kliens, sem a szolgáltatás, mivel ők nem ismerik a körülményeket, ezért egy külső komponensnek kell megadnia a megvalósítást.
A kliens (client) számára a megfelelő szolgáltatás (service) külső átadásának egy lehetséges módja a függőség befecskendezés.
A kliens biztosít egy átadási pontot a szolgáltatás interfésze számára, ahol a végrehajtás során a szolgáltatás megvalósítását adhatjuk át.
Az átadási pont függvényében 3 típusa lehet: konstruktor, metódus (beállító művelet), interfész (a kliens megvalósítja a beállító műveletet)
A befecskendést végző komponens (injector) lehet egy felsőbb réteg, vagy a rétegződéstől független környezeti elem.
Factory
A gyártó (factory) egy olyan objektum, amelynek feladata más objektumok előállítása műveletek segítségével.
Lehetőséget ad objektumok példányosításánál:
- a konkrét példányosítandó típus kiválasztására
- a példányosítással járó kódismétlés kiküszöbölésére
- fel nem fedhető környezeti információk használatára
- a példányosítási lehetőségek bővítésére
Lehetővé teszi a konkrét legyártott típus cseréjét a gyártó művelet és az absztrakt gyártó segítségével.
Amennyiben több, kapcsolatban álló típus konkrét megvalósítását szabályoznánk, az absztrakt gyártó (abstractfactory) tervmintát használhatjuk.
Command
A háromrétegű architektúrában a nézet továbbra is összetett, de a tevékenységek leválaszthatóak, a parancs (command) tervminta lehetőséget ad egy művelet kiemelésére egy külön objektumba.
- a végrehajtandó tevékenység (Action) formája, paraméterezése tetszőleges lehet, ezért nem lehet egyazon módon különböző környezetekben kezelni
- a parancs (Command) egy egységes formát biztosít egy tevékenység végrehajtására (Execute), a konkrét parancs (ConcreteCommand) pedig végrehajtja a tevékenységet
- a kezdeményező (Invoker) csupán a parancsot látja, így a tényleges végrehajtás előle rejtett marad.
Observer
A figyelő (observer) tervminta célja összefüggőség megadása az objektumok között, hogy egyik állapotváltozása esetén a többiek értesítve lesznek
- a figyelő (Observer) ehhez biztosítja a változás jelzésének metódusát (Update)
- a megfigyelt objektumok (Subject) az értékeikben tett változtatásokat jelzik a felügyelőknek (Notify)
- egy objektumot több figyelő is nyomon kísérhet
Az alapelvek hatása az architektúrára
Az alapelveket a tervezés minden szintjén, így az architektúra szintjén is célszerű betartani.
- Monolítikus architektúra esetén egyáltalán nem érvényesülnek az alapelvek.
- Modell-nézet architektúra esetén is túl nagy a komponensek
felelőssége:
- A modell felel az üzleti logikáért (programállapot kezelése, algoritmusok végrehajtása), valamint az adatok hosszú távú tárolásáért (mentés, betöltés)
- A nézet felel az adatok megjelenítéséért, valamint a vezérlésért (felhasználó tevékenység fogadása és feldolgozása)
Háromrétegű architektúra
A modell felbontásával jutunk a háromrétegű (3-tier) architektúrához, amelyben elkülönül:
- a nézet (presentation, view, display)
- a modell (logic, business logic, application, domain), amely tartalmazza az állapotkezelést, valamint az algoritmusok
- a perzisztencia, vagy adatelérés (data, dataaccess, persistence), amely biztosítja a hosszú távú adattárolás (pl. fájl, adatbázis) kezelését
Adatok állapotai
A háromrétegű alkalmazásokban az adatok három állapotban jelennek meg.
- megjelenített állapot (display state): a felhasználói felületen megjelenő tartalomként, amelyet a felhasználó módosíthat
- munkafolyamat állapot (session state): a memóriában, amely mindaddig elérhető, amíg a program és felhasználója aktív
- rekord állapot (record state): az adat hosszú távon megőrzött állapota az adattárban (perzisztenciában)
Adatkötés
Az állapotok között a programnak transzformációkat és szinkronizációt kell végeznie
- a nézet állapot és a munkafolyamat állapot sokszor megegyezik, a munkafolyamat és a perzisztens állapot (adattárolási forma) sokszor különbözik, ezért külön adatelérést kell biztosítanunk
- a munkafolyamat és a perzisztens állapot között általában ritkán történik szinkronizáció (pl. program indítása, leállítása)
- a nézet állapot és a munkafolyamat állapotot rendszerint állandó szinkronban kell tartanunk, ezt lehetőség szerint automatizálnunk kell
Az állapotok automatikus szinkronizálását adatkötés (data binding) segítségével érhetjük el, amely két lehetséges módon biztosíthatja a szinkronizációt.
Az adatkötésért egy olyan adatkötés objektum (Binding) felel, amelyet a megjelenített állapot tárolója (nézet) és a munkafolyamat állapot tárolója (modell) közé helyezünk
- az adatkötés ismeri mind a nézetet mind a modellt, ezért lehívhatja az értékeket (GetState), és elvégezheti a módosítást (SetState)
- elvégezheti az átalakítást (Convert) a munkafolyamat állapot és a nézet állapot között
- általában minden szinkronizálandó adathoz külön adatkötés tartozik, többszörös előfordulás esetén akár előfordulásonként is tartozhat adatkötés
A nézet ismerheti az adatkötést, így közvetlenül kezdeményezheti a módosítást az adatkötésen keresztül.
A modell azonban nem ismerheti az adatkötést, sem a vezérlőt, csak jelzést tud adni az állapot változásáról, ennek feldolgozását figyelő tervminta segítségével végezzük.
Az adatkötés megvalósítja a figyelőt, ám mivel közvetlenül nem ismerheti a modell, a változás jelzése esemény formájában történik (NotifyStateChanged).
Mivel a jelzésnek egységes formában kell megvalósulnia, célszerű, ha minden modell egy közös, az esemény kiváltását biztosító interfészt valósít meg (Subject).
Előnyei:
- a megjelenített és a munkafolyamat állapot mindig szinkronban tartható, automatikusan
Hátrányai:
- a szinkronizáció erőforrásigényes, sokszor feleslegesen hajtódik végre
- a rendszernek ügyelnie kell a körkörös módosítások elkerülésére
- a modellnek biztosítania kell a megfelelő interfész megvalósítását, és az esemény kiváltását a szükséges pontokon
MVC architektúra
A megjelenítés és a vezérlés leválasztását biztosítja a Model-View-Controller (MVC) architektúra, amelyben
- a vezérlő (Controller) fogadja közvetlenül a kérést a felhasználótól, feldolgozza azt (a modell segítségével), majd előállítja a megfelelő (új) nézetet
- a nézet (View) a felület (jórészt deklaratív) meghatározása, amely megjeleníti, illetve átalakítja az adatokat
- lehívás alapú (pull-based): ismeri a modellt, az adatokat a modelltől kéri le
- betöltés alapú (push-based): a vezérlő adja át számára az adatokat
A modell mellett perzisztációval is bővíthető a szerkezet.
Az MVC architektúra különösen webes környezetben népszerű, ahol könnyen leválasztható a nézet (HTML) a vezérléstől (URL) Általában egy vezérlőhöz több nézet is tartozik.
Előnyei:
- a nézetnek nem kell foglalkoznia az események feldolgozásával, mivel azokat közvetlenül a vezérlő kapja meg
Hátrányai:
- a nézet továbbra is felel az adatok megfelelő átalakításáért, tehát tartalmaz valamennyi logikát
Források
Projekteszközök, verziókezelés
Projektmenedzsment eszközök
Szoftvereszközök
A fejlesztőcsapat munkáját megfelelő szoftvereszközökkel kell alátámasztani
- projektmenedzsment eszközzel (project tracking system), amely támogatja a dokumentálást és a feladatok követését
- fejlett tervezőeszközzel (case tool), ahol a fejlesztés folyamata és a felelősség is nyomon követhető
- integrált fejlesztőkörnyezettel (IDE)
- verziókövető rendszerrel (revision control system), amely lehetővé teszi a programkód változásainak követését
- folytonos integrációs (continuous integration) rendszerrel, amely biztosítja a hibák korai kiszűrését
A projektmenedzsment eszköz lehetőséget ad az alábbiakra:
- fejlesztés ütemtervének, kockázatainak meghatározása
- fejlesztés egyszerű és folyamatos dokumentálásának lehetősége és generálása
- feladatok, tevékenységek rögzítése, követése
- a tesztelés során előfordult hibák rögzítése, a javítási folyamat követése
- integrált verziókezelés és forráskód böngészés
- webes vagy grafikus felület, amely biztosítja a könnyű használatot, és bárhonnan való elérést
Ütemterv és időzítés
A szoftver lehetőséget ad, hogy a projekt ütemtervét elkészítsük, és azt folyamatosan szem előtt tarthassuk
- definiálhatunk mérföldköveket (milestone), amelyre adott feladatokat el kell végezni
- a fejlesztők külön-külön láthatják a saját feladataikat, menedzselhetik annak előrehaladását
- beoszthatjuk a fejlesztési lépések erőforrásait
- definiálhatunk függőségeket a programrészek között
- kezelhetjük az egyes fejlesztési lépések időbeli lefolyását, előrevetíthetjük a tervezettől való eltérések hatásait az erőforrásokra, illetve a további fejlesztési időkre
Feladat és hibakövetés
A rendszerek lehetőséget adnak a tervezők számára feladatok kitűzésére, valamint a tesztelők számára a programban fellelhető hibák jelzésére
- a feladatokat úgynevezett cédulák (ticket, issue)
segítségével írhatóak ki
- jelölhetnek új funkcionalitást (feature), hibát (bug), egyéb fejlesztési feladatot (task), vagy dokumentációs feladatot (documentation)
- megadható a leírása, felelőse, határideje
- kommentálhatóak, lezárhatóak, újra kinyithatóak
- a cédulák biztosítják a fejlesztési és tesztelési folyamat naplózását
Projektvezető szolgáltatások
A projektvezető szolgáltatások (project hosting services) általában rendelkezésre bocsátanak több projektfejlesztő eszközt
- projektmenedzsment, kód tárolás, kód megtekintés, verziókövetés, dokumentáció (Wiki), levelezési lista, adatbázis hozzáférés
- általában nyílt forráskódú szoftverek esetén ingyenes a szolgáltatás
- pl.:GitHub, GitLab, SourceForge, Bitbucket
- egyes szolgáltatások bizonyos programozási nyelvek, vagy témakör köré csoportosulnak (pl. mozdev)
Verziókezelés
A szoftverek méretének és komplexitásának növekedésével létrejött szoftverkrízis következményeként megnövekedett:
- a programok forráskódjának mérete,
- a szoftverprojektek megvalósításához szükséges idő,
- és szükséges programozói erőforrás.
A szoftveripar fejlődésével egyre több alkalmazás készült
- a fejlesztések életciklusa gyakran nem ért véget a program első publikus verziójának kiadásával,
- karbantartási és további fejlesztési fázisok követték.
A szoftverprojektek méretben, komplexitásban, időben és a résztvevő fejlesztők számában is növekedni kezdtek.
Történeti háttér
Mivel az implementáció tehát több lépésben, és sokszor párhuzamosan zajlik, szükséges, hogy az egyes programállapotok, jól követhetőek legyenek, ezt a feladatot a verziókövető rendszerek (revision control system) látják el
- pl. CVS, Apache Subversion (SVN), Mercurial, Git
- egy közös tárolóban (repository) tartják kódokat
- ezt a fejlesztők lemásolják egy helyi munkakönyvtárba, és amelyben dolgoznak (working copy)
- a módosításokat visszatöltik a központi tárolóba (commit)
- a munkakönyvtárakat az első létrehozás (checkout) után folyamatosan frissíteni kell (update)
Funcionalitás
A verziókövető rendszerek lehetővé teszik:
- az összes eddig változat (revision) eltárolását, illetve annak letöltési lehetőségét
- a fő fejlesztési vonal (baseline, master vagy trunk) és a legfrissebb változat (head) elérését, új változat feltöltését annak dokumentálásával
- az egyes változatok közötti különbségek nyilvántartását fájlonként és tartalmanként (akár karakterek szintjén)
- változtatások visszavonását, korábbi változatra visszatérést
- konfliktust okozó módosítások ellenőrzését, illetve megoldását (resolve)
- a folyamat elágazását, és ezáltal újabb fejlesztési
folyamatok létrehozását, amelyek a fő vonal mellett futnak
(branch), valamint az ágak összeillesztését (merge)
- az összeillesztés rendszerint utólagos manuális korrekciót igényel
- az összeillesztésnek rendszerint automatikusan illeszti a módosított tartalmakat kódelemzést használva, ez lehet 2 pontos (two-way), amikor csak a két módosítást vizsgálja, vagy 3 pontos, amikor az eredeti fájlt is
- programrészek zárolását (lock), hogy a konfliktusok kizárhatóak legyenek
- adott verzió, mint pillanatkép (snapshot) rögzítése (tag), amelyhez a hozzáférés publikus
- feltöltések atomi műveletként történő kezelését (pl. megszakadó feltöltés esetén visszavonás)
Lokális verziókövető rendszerek
Forráskód változásainak követése, a szoftver funkcióinak különböző kombinációjával készült kiadások kezelése
- lokális tároló (de többen is elérhetik pl. mainframe esetén)
- fájl alapú műveletvégzés (1 verzió 1 fájl változásai)
- konkurenciakezelés kizárólagos zárak által
Az 1970-es években lefektetésre kerültek az elméleti alapok
- Source Code Control System (SCCS) – 1972
- Revision Control System (RCS) - 1982
Centralizált verziókezelő rendszerek
Több fejlesztő általi párhuzamos szoftverfejlesztés támogatásának előtérbe kerülésre
- centralizált modellt megtartva, de kliens-szerver architektúra
- fájlhalmaz alapú műveletek (1 verzió több fájl változásai)
- konkurenciakezelés jellemzően beküldés előtti egyesítéssel (merge before commit)
Az 1990-es évektől terjedtek el:
- Concurrent Versions System (CVS)
- Subversion (SVN)
- SourceSafe, Perforce, Team Foundation Server, stb.
Hátrány: a szerver kitüntetett szerepe (pl. meghibásodás), továbbá a verziókezeléshez hálózati kapcsolat szükségeltetik
Elosztott verziókezelő rendszerek
A klasszikus verziókezelő műveletekről leválasztásra kerül a hálózati kommunikáció, azok a felhasználó által kezdeményezhető önálló tevékenységekként jelennek meg
- decentralizált, elosztott hálózati modell
- minden kliens rendelkezik a teljes tárolóval és verziótörténettel
- a revíziókezelő eszköz műveletei lokálisan, a kliens tárolóján történnek
- a kommunikáció peer-to-peer elven történik, de kitüntetett (mindenki által ismert) szerverek felállítására van lehetőség
- konkurenciakezelés jellemzően beküldés utáni egyesítéssel (commit before merge)
A 2000-es évek első felében jelent meg:
- Monotone, Darcs, Git, Mercurial, Bazaar, stb.
Változások reprezentációja
A teljes revíziók tárolása nem lehetséges az adattárolás és adatkezelés jelentős költségei miatt
A verziókezelő eszközök ezért csak két egymást követő verzió közötti különbséget, a változáslistát (changeset, delta) tárolják
- egyes rendszerek (pl. Mercurial) időnként pillanatfelvételt (snapshot) készítenek a teljes tartalomról
Eleinte (SCCS) a delták a régi verzióból az újat tudták előállítani (forward deltas)
Korán felmerült (RCS), hogy a fordított delták (reverse deltas) használata a legújabb verzió pillanatképének tárolásával jobb teljesítményt nyújthat, ugyanis leggyakrabban egy ág legfrissebb állapotát szokták lekérni
- Kevert megoldás is lehetséges, pl. a fő ágon fordított irányú deltákat, a mellékágakon viszont előre mutató delták
Az eltérések meghatározása szöveges fájlok, így programnyelvi forráskódok esetében jellemzően állapot alapúan történik
- a legtöbbször soronkénti összehasonlítással
- pl. GNU diff
- struktúrált tartalom esetén az összehasonlítás egysége más is lehet (pl. XML, JSON, UML)
Bináris adatok (pl. képek) esetén a művelet alapú megközelítés is alkalmazható.
A 3. generációs verziókövető rendszerek idejére a háttértárak mérete jelentősen megnőtt, míg költségük csökkent
- Egyes eszközök ezért a megváltozott fájlok teljes tartalmát tárolják a revíziókban, nem csak a módosult tartalomrészt
Külömböző fájlok tárolása
A Git verziókezelő rendszer a szöveges állományok, így tipikusan a forráskód fájlok változáskezelésében hatékony. Elsődlegesen a projekt forráskódját érdemes benne elhelyezni.
Egy általános szoftver projekt esetén nem érdemes verziókezelés alá vonni:
- fordítás során előálló köztes tárgykódot vagy a végső bináris állományokat, mert újból előállíthatóak, folyamatosan változnak és ütközéseket okoznak.
- fejlesztő eszközök személyes beállításait (pl. Visual Studio esetén a .vs/ vagy Netbeans esetén a nbproject/private/ könyvtárak), amelyek felhasználónként eltérőek.
- nagy méretű bináris állományokat (pl. videók, nagy méretű képek), amelyek kezelésében a Git nem hatékony. Bár a Git tárolók mérete jól skálázható, egy könnyen kezelhető repository mérete az 1-2 GB-os méretet nem haladja meg.
A nagy méretű videó, kép és hang erőforrás állományok hatékony kezelése körültekintést igényel.
- A nagy méretű bináris állományok változásainak kezelésében a Git kevésbé hatékony.
- Jelentősen megnöveli a tároló helyi másolatának lekéréséhez szükséges hálózati forgalmat (git clone).
- Egy fejlesztőcsapatban a programozóknak nem feltétlenül van szükségük a fejlesztéshez a designerek által készített assetekre.
Ezért a nagy méretű bináris erőforrás állományokat még akkor sem feltétlenül érdemes a Git tárolóban elhelyezni, ha amúgy ritkán változnak.
A nagy méretű bináris állományok kezelése a Git Large File Storage (Git LFS) segítéségével oldható meg.
- A nagy méretű bináris állományokat egy hivatkozással helyettesíti és magukat a fájlokat egy másik (akár távoli) szerveren tárolja.
- Így a Git tárolónk mérete kezelhető marad.
Gitflow feature branching model
Fő fejlesztési ágak:
- master
- develop
Támogató ágak:
- feature branches
- release branches
- hotfix branches
Források
Build systems
Java programok fordítása
Már viszonylag kevés forrásfájllal is nehézkes lehet:
- Parancssoros fordítás könnyen bonyolultá válhat már kis alkalmazásoknál is.
- Nagyobb programoknál követhetetlenné válik, hogy mely fordítási egységeket kell újrafordítani.
- Az egész alkalmazást újra lefordítani nagyon időigényes lehet.
Build system elvárások
- A kód fordítása
- Dependenciák a fordítási target-ek kezelése
- Futtatható fájlok csomagolása
- Több release opció támogatása
- Automatikus tesztfuttatás
- Futtatható fájlok feltöltése teszt szerverre
- A kód átmásolása egyik helyről a másikra
- Csomag repo-k kezelése
ANT
-
Imperatív megközelítés
-
Java projektekhez gyakran használt
-
XML-alapú build fájl
- tartalmazza a project gyökér elemet amely megadja:
- a projekt nevét,
- az alapértelmezett target-et
- A projekt főkönyvtárát
- tartalmazza a project gyökér elemet amely megadja:
-
A
<property name="" value="">elemmel projekttulajdonságokat tudunk definiálni.
Target
- Target-et a
<target>elemmel lehet megadni, és azant compileparancsal futtatni. - Egy target függhet egy másiktól, ezt a
<target depends="">módon lehet megadni. - A
failonerrorattribútum megmondja, hogy hiba esetén félbe kell-e szakítani a folyamatot, ha az adott target hibát dob.
További példák
lsd.: diasor
Maven
- Szoftver projekt kezelő eszköz
- Build, teszt futtatás, dependencia kezelés, dokumentáció
- Csomagok: automatikus letölti a dependenciákat
- Deklaratív leírása a build folyamatnak
- Fix könyvtár struktúra és konvenciók
- Ezek átírhatók, de nem ajánlott
- Tipikusan Java-hoz, de pluginokkal használható más nyelvekkel is
- XML-alapú build fájl
Project
- POM - Project Object Model
- Egy projektet egyedien azonosít a csoport, artifact id, verzió. (GAV - Group, Artifact, Version)
- Egy projekt felosztható több modulra, amik külön-külön kezelhetőek.
POM
-
Részei:
- azonosítók:
groupId, artifactId, version - a build folyamatának leírása
- a build eredménye
- tesztesetek
- dependenciák
- azonosítók:
-
A gyökérelem szintén egy project element.
-
A következő elemeknek meg kell lenniük a projektben:
modelVersion: a POM specifikáció verziójagroupId: egyedi csoport, vagy cégazanosító. Ajánlott a Java package elnevezési konvenciók követése.artifactId: a projekt egyedi neveversion: a projekt verziószámapackaging: alkalmazott csomagolási módszer (alapértelmezett: jar, mások: pom, maven-plugin, ejb, war, ear, rar, par)
Életciklus fázisok
- Maven egy előre meghatározott életciklust követ, amely különböző fázisokból áll. A legfontosabbak:
- validate: validálja a projektet, és meggyőződik arról, hogy minden szükséges információ rendelkezésre áll.
- compile: lefordítja a projektet
- test: leteszteli a lefordított kódot (a forrásfájlok nélkül)
- package: a lefordított kód becsomagolása a megadott formátumban (pl.: JAR)
- integration-test: a csomag feldolgozása és megfelelő tesztelési környezetbe helyezése, ahol integrációs tesztek futtathatók.
- verify: a csomag ellenőrzése, hogy megfelel-e a minőségi kritériumoknak
- install: a csomag telepítése a lokális repo-ba, hogy dependenciaként használható legyen lokálisan
- deploy: integrációs vagy release környezetbe helyezés, távoli repo-ba feltöltés.
- clean: előzően létrehozott bináris fájlok törlése a projektből
Goal
- A fordítási fázisok egy vagy több goal-ból áll
- A goal egy olyan feladat, ami a projekt kezeléséhez vagy fordításához kapcsolódik.
- Ezek sorrendje a fázis kötésétől függ
- Sokfázis csak egy goal-t tartalmaz
- Nem csak fázisok, de goal-ok is futtathatóak a maven paranccsal.
Repositories
- Egy repo tartifact-okat és dependenciákat tárol.
- Ha egy artifact elérhető lokális repo-ban, Maven azt használja
- Különben letölti egy távoli repo-ból. (lassabb)
A build folyamat eredménye
- a
targetkönyvtár létrehozásra kerül fordítás során, amely az újonnan generált fájlokat tartalmazza- kiement, pl.: my-app-1.0.jar
classeskönyvtár: class fájlok, amelyek a fordítás során jöttek létre (kivéve teszt osztályok)test-classes: teszt osztályokmaven-archiver/pom.propertiesfájl, ami definiálja a project GAV-játsurefire-reports: a tesztek eredményei
Dependenciák
- Külső könyvtáral amit a projekt használ
- Automatikus letöltés, ha kell
- GAV egyedien definiálja a szükséges artifact-ot
- Egy scope megadja a felhasználás módját:
- compile: ez az alapértelmezett, a dependencia szükséges a fordításhoz
- runtime: a dependencia futásidőben szükséges, de fordításkor nem
- test: a dependencia nem kell csak tesztek fordításánál és végrehajtásánál.
Gradle
- Build automatizáló rendszer amely egyre elterjedtebb
- Azt ANT és a Maven-t legjobb tulajdonságait próbálja ötvözni.
- Inkrementális build támogatás
- XML helyett Groovy alapú nyelven (Domain Specific Language)
Források
Verifikáció és validáció
Minőségbiztosítás
A szoftver verifikációja és validációja, vagy minőségbisztosítása azon folyamatok összessége, amelyek során ellenőrizzük, hogy a szoftver teljesíti-e az elvárt követelményeket, és megfelel a felhasználói elvárásolnak.
- A verifikáció ellenőrzi, hogy a szoftvert a megadott funkcionális és nem funkcionális követelményeknek megfelelően valósították meg. Történhet formális, vagy szintaktikus módszerekkel.
- A validáció ellenőrzi, hogy a sziftver megfelel-e a felhasználók elvárásainak, azaz jól specifikáltuk-e eredetileg a követelményeket. Alapvető módszere a tesztelés.
Verifikáció és modifikáció módszerei
- Statikusan, a modellek és a programkód áttekintésével
- elvégezhető a teljes program elkészülte nélkül is
- elkerüli, hogy hibák elfedjék egymást
- tágabb körben is felfedhet hibákat, pl. szabványoknak történő megfelelés.
- Dinamikusan, a program futtatásával.
- felfedheti a statikus ellenőrzés során észre nem vett hibákat, illetve a programegységek együttműködéséből származó hibákat.
- lehetőséget ad a teljesítmény mérésére
Tesztelés
A tesztelés célja a szoftverhibák felfedezése és szoftverrel szemben támasztott minőségi elvárások ellenőrzése.
- futási idejű hibákat, működési rendellenességeket keresünk, kompatibilitást ellenőrzünk.
- általában a program futtatásával, szimulált adatok alapján történik.
- nem garantálja, hogy a program hibamentes, és minden körülmény között helytáll, de felfedheti a hibákat adott körülmények között.
A teszteléshez tesztelési tervet készítünk, amely ismerteti a tesztelés felelőseit, folyamatát, technikáit és céljait.
Tesztesetek
A tesztelés során különböző teszteseteket különböztethetünk meg, amelyek az egyes funkcióját, illetve elvárásokat tudják ellenőrizni.
- megadjuk a bemenő adatokra várt eredményt
- a teszteseteket összekapcsolhatjuk a követelményekkel (traceability matrix)
- a teszteseteket gyűjteményekbe helyezzük (test suit) A tesztesetek eredményeiből készül a tesztjelentés (test report)
Tesztelés lépései
A tesztelés nem a teljes program elkészülte után, egyben történik, hanem általában 3 szakaszból áll:
- fejlesztői teszt: a fejlesztők ellenőrzik a program működését
- jellemzően white box tesztek, azaz a fejlesztő ismeri, és követi a programkódot.
- kiadásteszt: egy külön tesztcsapat ellenőrzi a szoftver használatát
- felhasználói teszt: a felhasználók tesztelik a programot a felhasználási környezetben
- jellemzően black box, azaz a forráskód nem ismert.
A fejlesztői tesztnek további három szakasza van:
- unit test: a programegységeket külön-külön, egymástól függetlenül teszteljük.
- integrációs teszt: a programegységek együttműködésének tesztje, a rendszer egy komponensének vizsgálata
- rendszerteszt: az egész rendszer együttes tesztje, a rendszert alkotó komponensek közötti kommunikáció vizsgálata
Unit tests
Az egységteszt során törekednünk kell arra, hogy a programegység összes funkcióját ellenőrizzük, egy osztály esetén
- ellenőrizzük valamennyi metódust
- állítsuk be, és ellenőrizzük az összes mezőt
- az összes lehetséges állapotba helyezzük az egységet
A teszteseteket célszerű leszorítani a programegység által
- megengedett bemenetekre, így ellenőrizve a várt viselkedést
- nem megengedett bemenetre, így ellenőrizve a hibakezelést
A bemenő adatokat részhalmazokra bonthatjuk a különböző hibalehetőségek függvényében, és minden részhalmazból egy bemenetet ellenőrizhetünk.
Az egységtesztet az ismétlések és a számos kombináció miatt célszerű automatizálni.
Előnyök
- A hibák sokkal korábban észlelhetőek
- Minden komponens legalább egyszer tesztelt
- Az egységek elkülönítése miatt a hibák helyének meghatározása könnyű
- A funkciók könnyen módosíthatóak, átalakíthatók
- Dokumentációs szerep: példákat biztosít egyes funkciók használatára
Elvek
- Gyors: A teszteknek gyorsan kell futnia, lassú teszteket senki nem futtatja gyakran, így a hibák nem derülnek ki idejében.
- Független: A teszteknek egymástól függetlennek és bármilyen sorrendben végrehajthatónak kell lennie.
- Megismételhető: A teszteknek bármilyen környezetben, hálózat nélkül is végrehajthatónak kell lennie. A különböző futtatások eredményének meg kell egyeznie.
- Önellenőrző: A tesztek eredménye egy logikai érték (futásuk vagy sikeres, vagy sikertelen)
- Automatikus: Automatikusan, interakció nélkül futó tesztek
Mock
- A tesztelt metódusok általában más komponens nyújtotta szolgáltatásokat is használnak
- Az egyes funkciókat más komponensektől izoláltan kell tesztelnünk, a tesztek sikeressége nem függhet a függőségek helyes implementációjától
- A Mock egy olyan objektum, amely egy másik objektum működését szimulálja
- Egy osztály függőségeinek szimulálására használandó
Tesztelési keretrendszerek
Az egységtesztek automatizálását, és az eredmények kiértékelését hatékonyabbá tehetjük tesztelési keretrendszerek használatával.
- általában a tényleges főprogramoktól függetlenül építhetünk teszteseteket, amelyeket futtathatunk, és megkapjuk a futás pontos eredményét
- a tesztesetekben egy, vagy több ellenőrzés kap helyet, amelyek jelezhetnek hibákat
- amennyiben egy hibajelzést sem kaptunk egy tesztesettől, akkor az eset sikeres, egyébként sikertelen
Kódlefedettség
A tesztgyűjtemények által letesztelt programkód mértékét nevezzük kód lefedettségnek.
- megadja, hogy a tényleges programkód mely részei kerülnek végrehajtásra a teszt során
- számos szempont szerint mérhető:
- mely alprogramok lettek végrehajtva
- mely utasítások lettek végrehajtva
- az elágazások mely ágai futottak leű
- a logikai kifelyezések mely részei lettek kiértékelve
További tesztek
Az integrációs és rendszertesztek során elsősorban azt vizsgáljuk, hogy a rendszer megfelel-e a követelménybeli elvárásoknak.
- funkcionális és nem funkcionális alapon (pl. teljesítmény, biztonság) is ellenőrizhetjük a rendszert
- ezeket a teszteseteket már a specifikáció során megadhatjuk
- a tesztelés első lépése a füst teszt (smoke test), amely során a legalapvetőbb funkciók működését ellenőrzik
A kiadásteszt és a felhasználói teszt során a szoftvernek már általában a célkörnyezetben, tényleges adatokkal kell dolgoznia
Teljesítménytesztek
A teljesítménytesztek (performance test) során a rendszer teljesítményét mérjük
- ezáltal a rendszer megbízhatóságát és teljesítőképességének (válaszidők, átviteli sebességek, erőforrások felhasználása) ellenőrizzük különböző mértékű feladatvégzés esetén
- végezhetünk teszteket a várható feladatmennyiség függvényében (load test), vagy azon túl ellenőrizhetjük a rendszer tűrőképességét (stress test)
- a teljesítmény tesztet sokszor a hardver erőforrások függvényében végezzük, amellyel megállapítható a rendszer skálázhatósága (capacity test)
Debugging
A tesztelést elősegíti a nyomkövetés (debugging), amely során a programot futás közben elemezzük, követjük a változók állapotait, a hívás helyét, felfedjük a lehetséges hibaforrásokat
- breakpoint elhelyezése
- watch, amely automatikus lokális változókra
- call stack kezelése, a felsőbb szintek változóinak nyilvántartása
Programváltozatok
Az implementáció és tesztelés során a szoftver különböző változatait tartjuk nyilván:
- pre-alpha: funkcionálisan nem teljes, de rendszertesztre alkalmas
- alpha: funkcionálisan teljes, de minőségi mutatókat nem teljesíti
- beta: funkcionálisan teljes, és a minőségi mutatók javarészt megfelelnek a követelményeknek
- a további tesztelés során nagyrészt a rendellenességek kiküszöbölése folyik, a tesztelés lehet publikus
- esetlegesen kiegészítő funkciók kerülhetnek implementálásra
- release candidate: funkcionálisan teljes, minőséfi mutatóknak megfelelő
- kódteljes
- csak dinamikus tesztelés folyik, és csak kritikus hiba esetén nem kerül gyártásra
- final release: kiadott, legyártott változat
Tesztvezérelt fejlesztés
A tesztvezérelt fejlesztés egy olyan fejlesztési módszertan, amely a teszteknek ad elsőbbséget a fejlesztés során
A fejlesztés lépései:
- tesztesetek elkészítése, amely ellenőrzi az elkészítendő kód működését
- az implementáció megvalósítása, amely eleget tesz a teszteset ellenőrzéseinek
- az implementáció finomítása a minőségi elvárásoknak (tervezési és fejlesztési elvek) megfelelően
Előnye, hogy magas fokú a kód lefedettsége, mivel a teszteknek minden funkcióra ki kell térniük.
Források
8. CI/CD - nincs jegyzet
9. Test Driven Development, Clean Code
10. Szálak - nincs jegyzet
11. Tervminták - nincs jegyzet
12. Networking - nincs jegyzet
Szoftvertechnológia (F) gyakorlat
Alapadatok
Idő: Hétfő, 12:00 - 14:00
Helyszín: Déli Tömb 00-411 (PC 7)
Oktató: Pintér Balázs
Csoport: 8
Értékelés
- 3 fős csapatok, scrum módszertan
- Mérföldkőbemutatás (4db)
Források
1. Gyakorlat
A VCS-ek alapjairól és git-parancsokról beszéltünk. Kialakítottuk a csapatot.
Források
2. Gyakorlat
Kiválasztottuk az opcionális feladatok közül 3 pontnyit.
3. Gyakorlat
Kigyűjtöttük az asset-eket
4. Gyakorlat
- mérföldkő bemutatása
5. Gyakorlat
Javított osztálydiagram bemutatás
6. Gyakorlat
GUI progress bemutatás, perzisztencia megbeszélés
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
8. Gyakorlat
- mérföldkő bemutatása
9. Gyakorlat
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
12. Gyakorlat
Számítógépes grafika előadás
Alapadatok
Idő: Szerda, 8:00 - 10:00
Helyszín: Déli Tömb 0-823 Kitaibel Pál terem
Oktató: Bán Róbert, robert.ban102+cg@gmail.com
Csoport: 1
Értékelés
Két írásbeli részvizsga alapján:
- Első az anyag felénél, második a félév végén
- Kb. 50%-50% elméleti és gyakorlati feladatok
Források
Ajánlott irodalom
Bevezetés a számítógépes grafikába
- Bevezetés a számítógépes grafikába
Számítógépes grafika
Kép előállításának lépései
- Reprezentáció: számítógépen való tárolás
- Szintézis: reprezentáció megjelenítése
- Megjelenítés: megfelelő megjelenítő eszköz használata
Modellezés "rétegei"
- Geometriai modellek
- Optikai paraméterek
- Textúrák (generált, mért, fényképezett)
Algoritmusok
- Sugárkövetés (ray tracing)
- Inkrementális képszintézis
Az emberi látás
Képek leggyakrabban két fő céllal szintetizálunk:
- Számtógép számára: egy leirást kell csupán megadni (hol, milyen szín van).
- Ember számára: meg kell jeleníteni a képet ehhez tisztában kell lenni az emberi látás tulajdonságaival, hogy minél kevesebb torzuláson essen át az átadni kívánt információ.
A képszintézissel az a célunk, hogy megadjuk hogy adott helyen milyen színt kell, hogy megjelenítsen a kijelző. Fontos ezért, hogy absztrakt és konkrét leírást is tudjunk adni.
A fény tulajdonságai
- Fénytörés:
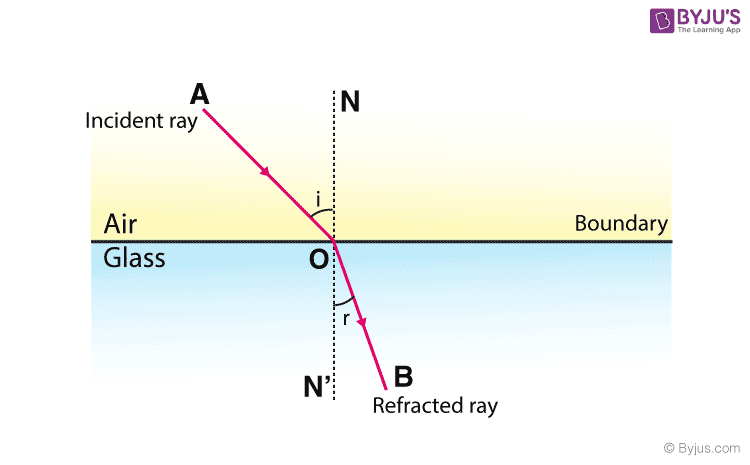
- Visszaverődés:
- Kromatikus aberráció:
- Hullám: elektromágneses sugárzás

- Részecske: fotonok

A látás fiziológiája
Az emberi látásnak fiziológiai és pszcihológiai aspektusai is vannak, amelyekben a szem és az agy vesz részt.
A fény útja a szemben
- A fény a szaruhártyán megtörve jut a szembe - ez lényegében egy fény-gyűjtőlencse.
- A szivárványhártya (írisz) csökkenti a szembe jutó fény mennyiségét, a pupilla pedig fényreteszként funkcionál.
- A szemlencse a második gyűjtőlencse; a belépő fénysugarakat a recehártyára (retinára) fókuszálja.
A szem különböző részeit összesítve kb. 16-12.5mm fókusztávolságot jelent. Az átlagos emberi szem 24mm hosszú a szaruhártyától a retináig.
Fotoreceptorok
A retinában kétféle fény érzékelésre szolgáló idegsejt található:
- Pálcikák (rod): alacsonyabb intenzitású fényre érzékenyek, a sötét-világos megkülönböztetésére alkalmas, alacsonyabb felbontásúak.
- Csapok (cone): erősebb fényingert igénylő idegsejtek, a színlátást és az éleslátást szolgálják, tizedannyira érzékenyek a fényre, mint a pálcikák.
Az elektromágneses energia egy bizonyos sávjára érzékenyek csak a fenti idegsejtek (380-780nm közötti intervellum)
Amikor a fény ér egy fotoreceptort egy kémiai reakció indul el, aminek eredményeképp egy neurális jelet küldenek az agy felé, úgynevezett fotopigmentet.
Az egyes fotoreceptorok más-más mértékben reagálnak a különböző hullámhosszú fényekre:
- Pálcikák: hullámhossztól függően az ugyanolyan erős fényre adott reakció nagysága harang-görbe jellegű görbével írható le.
- Csapok: háromféle van belőlük (S, M, L); mindegyik különböző hullámhosszú fényre ad maximális reakciót, azoktól fokozatosan eltérőkre egyel kisebbet.
A fotopigmentek csak az érzékelés tényét rögzítik: pontos hullámhossz nem továbbítódik. (térbeli és frekvenciabeli felbontás trade-off)
Háromféle csap található a szembe:
- S csap: 420nm körüli fényre a legérzékenyebb (kék)
- M csap: 530nm körüli fényre a legérzékenyebb (zöld)
- L csap: 560nm körüli fényre a legérzékenyebb (vörös)
A fényreceptorok észleléseit a látóideg továbbítja az agy felé. A látóideg csatlakozási pontja a szemgolyóhoz a vakfolt, itt nincsenek sem csapok, sem pálcikák.
A látógödör, ami a vakfolttól oldalra található az éleslátás helye, a közepe a foveola, ahol kizátólag csapok találhatóak. (150000 csap/mm)

A fotoreceptorok jele
A fotoreceptor jele egyetlen fotonra csak néhány ms-ig tart, minden újabb beérkező foton hatása hozzáadódik az előzőhöz.
A receptor által leadott jel lényegében egy temporális átlag, egy low-pass filter, aminek vágási frekvenciája függ a megvilágítási körülményektől.
- Egy lassan villogó fényt külön-külön villanásként észlelünk
- Ha a felvillanások között eltelt idő egyre kisebb, akkor a fotoreceptorok által leadott jelek
"összetorlódnak" (critical flicker-frequency) folyamatos jelként érzékeljük.
- A flicker rate sok tényezőtől függ (háttérmegvilágítás, megjelenített kép nagysága, ...)
- Ideális esetben kb 60hz.
Színek a számítógépen
CIE: International Commission on Illumination: hogyan lehetne egy standard leírást adni arra, hogy egy ember miképp érzékeli a színeket.
A kísérletek egyik eredménye volt, hogy bármely szín előállítható három, megfelelő szín keverékeként.
Színtér: egy koordinátarendszer három "független" bázisvektorral.
Válasszunk három kellően távoli hullámhosszt, majd minden színérzetre adjuk meg, hogy három ilyen monokromatikus fénynyaláb milyen keverékéből áll össze. Ezek lesznek az adott színérzet tristimulus koordinátái.
RGB színtér
Egy additív színmodell. Legyen a három kiválasztott hullámhossz:
Legyen egy monokromatikus fénynyaláb.
Ekkor a hozzátartozó RGB értékek megadására használjuk az színillszető függvényeket.
A spektrum minden színe megadható? Nem.
Az ember által érzékelt minden szín megadható? Nem. (lsd. link a források között)

CMY(K) színtér
Egy szubtraktív színmodell. Nézzük az RGB kockában az eredeti tengelyekkel "szemközti" tengelyeket!
Ez a három tengely ugyanúgy kifeszíti a színteret.
Ezt használják színes nyomtatáshoz (K, a fekete itt válik relevánsá)

HSL és HSV
Amikor színekről beszélünk gyakran használunk olyan fogalmakat, hogy telítettség, élénkség, világosság vagy sötétség.
A színeket egy hengerrel adjuk meg, egy árnyalat (Hue), egy telítettség (Saturation), és egy fényesség (Lightness) vagy világosság (Value) segítségével.

Megjelenítő eszközök
Oszcilloszkóp
Az eszköz hátuljában található elektronágyú elektronokat bocsájt ki. Az elektronnyaláb útját elektromágnesekkel téríti el a vizsgált jel alapján.
Az eszköz elején lévő foszforrétegbe csapódó elektronok bocsájtják ki a fényt.
CRT monitor
Őse az oszcilloszkóp - azonos működési elv.
Az elektronnyaláb végigpásztázza a képernyőt másodpercenként többször is.
A sugár ereje adott pillanatban határozza meg a fényerőt.
Színek: három elektronágyú, a beesési szögkülönbségből adódóan érik a megfelelő színszűrővel rendelkező területet.
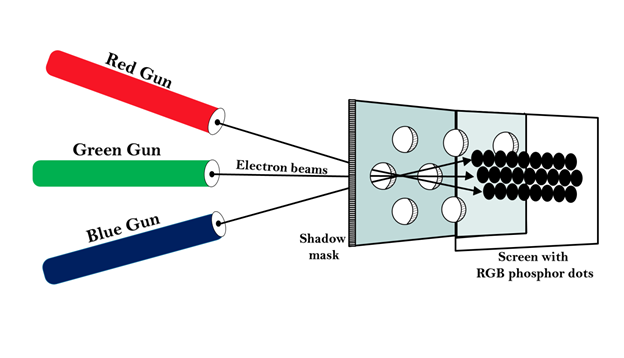
LCD monitor
Fehér háttérvilágítás polárszűrő folyadékkristály réteg, amely elektromos feszültség hatására különböző mértékben forgatja el a fény polarizáltságát.
Színek: minden színszűrőre különböző polarizáltságú fény jut.
Végül a korábbira merőleges polárszűrőn jut át a fény, így szabályozva a kijutó fény mennyiségét.
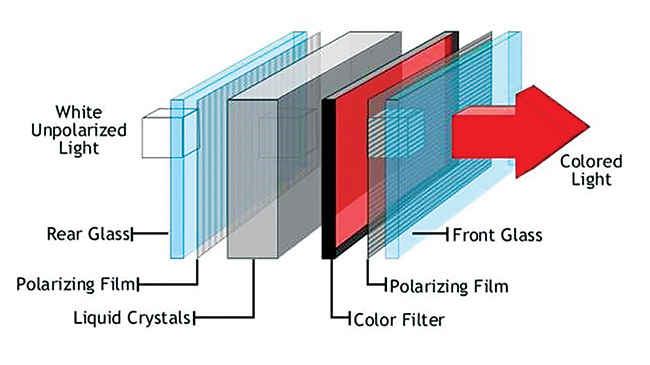
PDP kijelző (Plasma Display)
Minden képpont maga bocsájt ki fényt.
A pixelekben nemesgáz van, ami feszültség hatására világít, a neoncsőhöz hasonló elven.
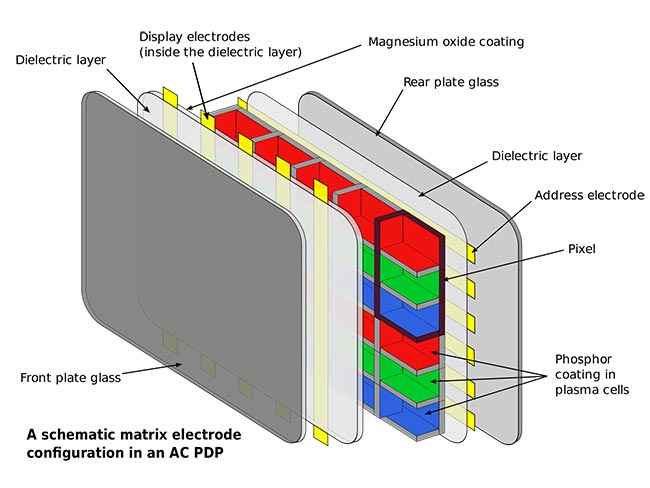
OLED kijelző
Minden pixel maga is fényforrás.
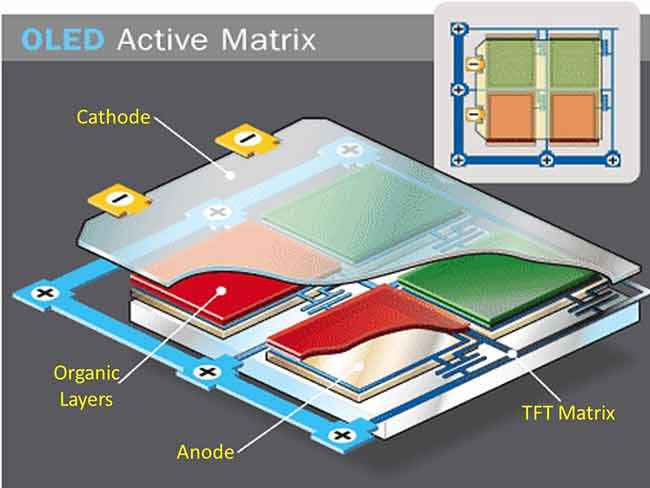
3D megkelenítők
- Stereoscopy:
- Mást lát a két szem, nincs mozgás parallaxis.
- Head mounted display
- Shutter glasses
- Polarizált lencséjű szemüveg
- Autostereoscopy:
- Nem kell hozzá külön eszköz a felhasználó részéről.
- Parallax barrier
- Lenticular lens
Raszter-, és vektorgrafika
Rasztergrafika
Az ábra legkisebb egysége a pixel, ami egy színt reprezentál.
A pixeleket valamilyen -es tömbben tároljuk.
Nagyításkor és kicsinyítéskor csak a pixelek látható méretét módosítjuk.
Vektorgrafika
A kép matematikailag leírható elemekből épül fel: görbék, síkidomok.
Ezekhez vannak rendelve különböző tulajdonságok: szín, kitöltés, vonalvastagság.
Az egyenes tényleg egyenes, a görbék bármilyen nagyítás alatt ívesek maradnak.
Források
- Diasor
- A mars-arc története
- Gernot Hoffmann: CIE Color Space
- CIE 1931 color space - Wikipedia
- Technology Connections: Weird world in RGB - youtube.com
Koordináta-rendszerek, egyenesek és síkok
- Koordináta-rendszerek, egyenesek és síkok
Alapfogalmak
Hogyan írjuk le a virtuális világunkat?
- A virtuális terünk egy pontját miként adjuk meg, hogyan tároljuk a számítógépen?
Koordináta-rendszerek - Az egyszerű geometriai komponenseket hogyan adjuk meg?
Pontok halmaza
leírás különböző koordináta-rendszerekben
Pontok, vektorok
Pont: az euklideszi sík/tér egy eleme, amelynek semmiféle kiterjedése sincs.
Vektor:
- algebrailag: egy vektortér eleme
- geometriailag: egy eltolás, aminek iránya és hossza van
- műveletei: összeadás, kivonás, skalárral szorzás, vektorális szorzat, skaláris szorzat
Vektororok összeadása
Legyen két vektor: .
Ekkor
Vektororok kivonása
Legyen két vektor: .
Ekkor
Vektor szorzata skalárral
Legyen a vektor: .
Ekkor
Vektororok skaláris szorzata
Legyen két vektor: és jelölje a skaláris szorzatukat.
Ekkor
Ez kifejezhető úgy is, hogy , ahol az és vektorok által bezárt szög.
Vektororok vektorális szorzata
Legyen két vektor: és jelölje a vektorális szorzatukat.
Ekkor
A vektorális szorzat kifelyezhető determinánsal is:
Egy pont és egy vektor is a választott koordináta-rendszerbeli koordinátáinak megadásával definiálható.
Műveletek pontok és vektorok között
- pont vektor pont pont eltolása
- pont pont vektor különbségvektor
- pont pont nincs értelmezve!
Ha pontokat, egyeneseket és síkokat veszünk, akkor ezeket különbözőnek tekintjük.
Jelölések
- Pontok:
- Vektorok:
- olyan vektor, amely egység hosszú
- Egyenesek:
- Síkok:
- Mátrixok:
Koordináta-rendszerek
A tér pontjainak egyértelmű leírására szám n-esek segítségével. pl.:
Lehetővé teszi az algebrai és analitikus eszköztár felhasználását geometriai problémák megoldására.
Egy, a problémához jól illeszkedő koordináta-rendszerben a probléma leírása egyszerűbb lehet.
Descartes koordináta-rendszer
Az euklidészi tér minden véges pontjához egyértelműen hozzárendel egy rendezett, valós számhármast.
A térben derékszögű koordináta-rendszert határoz meg egy kezdőpont (origó), és egy ortonormál bázis: három egymásra páronként merőleges egységvektor.
Ekkor egy pont koordinátái sorban az origóból a -be mutató vektor bázisvektorokra vett előjeles merőleges vetületével egyezik meg. (skaláris szorzat)
Vagyis a fenti értelmezés szerint, felhasználva az egységnyi hosszú, koordinátatengelyek irányába mutató bázisvektorokat, az koordináták a következő pontot azonosítják:
Sodrásirány (orientation)
Bal-, és jobbkéz szabály
Két pont távolsága
Vektor hossza
Polárkoordináta-rendszer
Egy kezdőpont (referenciapont) és egy abból induló félegyenes (polártengely) határozza meg.
Egy pont helyét két adat azonosítja: :
- : a pont -tól vett távolsága
- : az -ból induló -n átmenő félegyenes polártengellyel bezárt szöge
Általában akkor használjuk, ha az ábrázolni kívánt dolgokhoz jól illeszkedik, pl. körmozgás.
Hátrányai: egyik PKR-ből másikba áttérni költséges, deriváltak számítása szükséges.
Gömbi koordináták
Térbeli polár-koordináták; meghatározza egy alapsík (és annak PKR-r) illetve egy arra merőleges " tengely".
Egy térbeli p pontot három adat reprezentál:
- : a pont alapsíkra vett vetületének polárkoordinátái
- : az -ból kiinduló és -n áthaladó félegyenes tengellyel bezárt szöge
- : a pont és az origó távolsága. (ha akkor bármi lehet a két polárszög, konverziók előtt ellenőrizni kell)
Konverziók
Ha a Descartes origó és a polár referenciapont, illetve a Descartes x-tengely és a polártengely megegyezik:
- Polár Descartes:
- Descartes Polár:
Ha , akkor és emellett tetszőleges szöggel visszakapjuk az origót. Nem egyértelmű a polár szög, az -át még azelőtt ellenőrizzük, hogy a fenti konverziós képleteket próbálnánk használni.
A síknál látottakhoz hasonló feltételek mellett:
- Gömbi Descartes:
- Descartes Gömbi:
- , ha
- , ha
Baricentrikus koordináták
Sokszor egy konkrét, véges része érdekes csak számunkra a térnek. Ennek Descartes-félénél egy "kiegyensúlyozottabb" reprezentációját keressük.
A baricentrikus koordináták nem függnek egy pont önkényes orígónak választásától.
Tömegközéppont
Mechanikai analógia: pontrendszer tömegközéppontja
Legyen a síkban 3 pontunk és helyezzünk minden pontba súlyt.
Ekkor a tömegközéppont:
Homogén jellegű megadás: egy számmal megszorozva a súlyokat is ugyanazt a pontot kapjuk.
Ha -ben az pontok kifeszítik a teret (azaz nem esnek egy dimenziós altérbe), akkor a tér bármely pontjához egyértelműen találhatóak valós számok úgy, hogy
ahol a baricentrikus koordinátákra teljesül, hogy
(mivel súlyok)
Síkban tehát 3 általános állású pont kell (olyanok, amelyek nem esnek sem egyenesbe, sem pontba), a térben 4 általános állású pont kell.
Ha -re , akkor konvex kombinációról beszélünk és a pontok konvex burkába esnek a kombináció eredményei.
Az affin transzformációk nem változtatják meg a baricentrikus koordinátákat.
Síkbeli baricentrikus koordináta-rendszer
Legyen
A mennyiség az pontok által meghatározott háromszög előjeles területének duplája (pozitív, ha óra járásával ellentétes irányban adottak a csúcspontok, különben negatív)
Ha -ban vagyunk: , ahol a három pont síkjának egység hosszú normálisa.
Baricentrikus Descartes konverzió
- Baricentrikus Descartes:
- Legyenek egy pont baricentrikus koordinátái a
általános állású pontokra vonatkoztatva. - Ekkor az -vel azonosított pont Descartes koordinátái
, azaz
- Legyenek egy pont baricentrikus koordinátái a
- Descartes Baricentrikus:
- Egy pont baricentrikus koordinátái a következők lesznek a
általános állású pontokra vonatkoztatva:
- Egy pont baricentrikus koordinátái a következők lesznek a
Homogén koordináták
Motiváció
Egymással párhuzamos egyenesek nem találkoznak.
Ötlet: Bűvítsük ki -t!
tekintsük "pontnak" az egyenesek egyező állását (irányát) is, azaz minden egyenesnek legyen még egy "pontja".
Ez a pont az egyenes ideális pontja.
Ideális pont
Egyenes egyenes ideális pont úgy, hogy:
- Párhuzamos egyenesek ideális pontja megegyezik ("találkoznak a végtelenben")
- Egy sík ideális pontjai egy egyenesen vannak, ez a sík ideális egyenese
- Párhuzamos síkok ideális egyenese megegyezik
- A tér ideális elemei (pontok, egyenesek) egy síkban vannak, ez a tér ideális síkja.
Homogén tér
Homogén sík: az projektív lezárása, azaz egy kitüntetett ideális egyenessel
- Projektív síkban két pont meghatároz egy egyenest
- Két egyenes meghatároz egy pontot
Homogén tér: az projektív lezárása, azaz egy kitüntetett ideális síkkal
- Három pont meghatároz egy síkot
- Három sík meghatároz egy pontot
Az euklideszi tér minden pontjához hozzárendelünk egy számnégyest, homogén koordinátákat:
Az összes vektorhoz pedig:
Visszatérés Descartes koordináta-rendszerbe
Mit ábrázol az projektív térbeli elem?
- Ha , akkor egy közönséges pontról van szó, aminek koordinátái homogén (vagy projektív) osztás után
- Ha , de (nem mind nulla), akkor egy ideális pontról van szó, az vektorral egyező állású egyenesekhez rendeltről.
- Ha , akkor nincs értelmezve.
Nevezetes homogén alakok
Legyen tetszőleges, nem nulla valós szám. Ekkor a következő néhány példa nevezetes pontokra:
- az origó
- az tengely ideális pontja
- az tengely ideális pontja
- a tengely ideális pontja
Tulajdonságok
A projektív síkon a pont és az egyenes, a projektív térben a pont és a sík duális fogalmak.
Figyeljünk, hogy egyes tulajdonságok az euklideszi térből nem jönnek át:
- Egy egyenes egy pontja nem osztja két részre az egyenest! De két különböző pontja már két részre osztja
- Egy síkot csak egy egyenese nem osztja két részre! De két különböző állású egyenese már két részre osztja
- Két pontot összekötő egyenes szakasz sem egyértelmű! (az egyenes ideális pontja "összeregasztja" az egyenes két végét)
A homogén koordináták igen hasznosak lesznek transzformációs mátrixok használatánál, ugyanis a homogén koordináta "betartatja" a pontok és az eltolások közti műveletek szabályait.
Egyenesek és síkok leírása
Görbék, felületek
A görbéket, felületeket (amik közé az egyenes és a sík is tartozik) egy-egy ponthalmaznak tekintjük.
Hogyan adjuk meg ezeket a halmazokat?
- explicit: mi van ha vissza akarjuk "fordítani"?
- parametrikus:
- implicit:
Egyenes
Egyszerű képlet:
Probléma: mi legyen a függöleges egyenesekkel?
Normálvektoros egyenlet síkban
Az egyenes megadható egy pontjával és egy, az egyenes irányára merőleges
normálvektorral:
Az egyenes pontjai azon pontok, amelyek kielégítik a egyenletet.
Az és az egyenesünk által meghatározott két félsík pontjainak jellemzése.
Homogén, implicit egyenlet síkban
Az alakot hívjuk az egyenes implicit egyenletének.
A fentiek alapján és választással a ponton átmenő, normálisú egyenes implicit egyenletét kapjuk.
Ha , akkor Hesse-féle normalizált alakról beszélünk. Ekkor a korábbi normálvektor egység hosszúságú.
A homogén egyenlet determináns alakja
Ha az egyenesünket két, pontjával adjuk meg, akkor azon pontok fekszenek az egyenesen, amelyekre
Ez a determináns az pontok által meghatározott háromszög előjeles területének duplája, ami ha 0, akkor a három pint egy egyenesbe esik.
Parametrikus egyenlet irányvektorral (2D, 3D)
Az egyenes megadható egy pontjával és egy, az egyenes irányával megegyező irány irányvektorral:
Parametrikus egyenlet két pontal (2D, 3D)
Ekkor a és pontjait ismerjük az egyenesnek. Az előbbi esethez jutunk, ha választással élünk:
Homogén koordinátás alak
A kibővített (projektív) sík egy egyenese megadható az valós számhármassal, úgynevezett vonalkoordinátákkal, amelyeket felhasználásával az egyenes minden pontjára
A sík minden ideális pontjára illeszkedő ideális egyenes vonalkoordinátái
Polár koordinátás alak
Az origón áthaladó, a polártengellyel szöget bezáró irányú egyenesek polárkoordinátás (implicit) egyenlete:
Ha az egyenesünk nem halad át az origón, akkor legyen a metszéspontja az egyenesünknek és egy arra merőleges, origón áthaladó egyenesnek. Ekkor az egyenesünk polárkoordinátái közül a sugár a polárszög függvényeként felírható:
Sík
Normálvektoros egyenlet
A sík megadható egy pontjával és a síkra merőleges normálvektorával. Ekkor a sík minden pontjára:
Félterek:
Homogén, implicit alak
A sík implicit egyenletének alakja:
Előbbiből és
választással a ponton áthaladó, normálvektorú sík egyenletét kapjuk.
Hesse normál-alak itt is, ha
A homogén egyenlet determináns alakja
Determináns segítségével is megadhatjuk a sík egyenletét, a következő determináns csak pontok által kifeszített sík pontjaira lesz nulla:
Parametrikus egyenlet kifeszítő vektorral
A sík jellemezhető egy pontjával és két kifeszítő vektorával (bázisvektorával): ahol .
Parametrikus egyenlet három pontból
A síkot meghatározza három, nem egy egyenesbe eső pontja, . Ekkor a sík minden véges pontja megkapható.
alakban, ahol .
Az előbbiből is kaphatjuk ezt
Ez egy baricentrikus megoldás:
hiszen
Homogén koordinátás alak
A kibővített tér egy síkja is megadható "síkkordinátákkal", egy olyan négyessel, amely a sík minden pontjára
Nevezetes homogén alakú síkok
- az ideális sík
- az koordinátasík
- az koordinátasík
- az koordinátasík
Források
- Diasor
- Mátrix determináns
- Orientation (vector space) - wikipedia
- 2-norm - wikipedia
- atan2 - wikipedia
- Gamedev Maths: point in triangle - youtube (baricentrikus koordináták)
- Lineáris kombináció - wikipedia
- Affin transzformációk - wikipedia
- Homogén koordináták 5 percben - youtube
- GDC: Homogén koordináták - youtube
- Projectív geometria és homogén koordináták - youtube
- Krammer Gergely oldala - Koordinátarendszerek és transzformációk
Transzformációk
- Transzformációk
A virtuális világunkban található összetett alakzatokat több, kisebb építőelemből is összerakhatjuk az alakzat részeit el kell helyeznünk a térben.
Az alakzatokat el kell helyeznünk a világban, mozgatnunk kell őket, stb.
A virtuális világunkból egy kétdimenziós képet is elő kell állítanunk.
A fenti lépésekhez mind szükségünk lesz geometriai transzfotmációkra, amelyekkel az alakzatainkat megváltoztathatjuk.
Transzformációkról általában
Az elvárásaink:
- minden pontot lehessen transzformálni
- pont képe legyen pont, egyenes képe egyenes, sík képe sík
- illeszkedést tartsa
- legyen egyértelmű és egyértelműen megfordítható
A pontjainkat a számítógépen valamilyen koordináta-rendszerben tároljuk
a transzformációk ezeken a koordinátákon végzett műveletek.
A továbbiakban azonosítunk az euklideszi tér, elemeit a valós vektorterünk elemeivel.
Ehhez rögzítünk egy pontot, origót, és minden ponthoz a vektort rendeljük.
Lineáris leképzések
Kiemelt jelentősége lesz a lineáris leképzéseknek, azaz azon leképzéseknek, amelyekre teljesül, hogy és esetén
- (additív)
- (homogén)
Az lineáris leképzéseket egy mátrixszal fel tudjuk írni; ekkor
Projektív és affin transzformációk
Az ideélis síkkal kibővített euklideszi tér önmagára való, kölcsönösen egyértelmű, pont-, egyenes-, sík-, és illesztkedést tartó leképzéseit kollineacióknak, vagy projektív transzformációknak nevezzük.
Affin transzformációk a projektív transzformációknak az az alcsoportja, amelynek a kibővített tér "közönséges", euklideszi részét önmagára képzik le, és az ideális síkot is önmagára képzi le.
Közös tulajdonságok
A projektív és affin transzformációk algebrai csoportot alkotnak a konkatenáció művelettel
- a konkatenáció asszociatív (műveletek csoportosíthatóak)
- létezik egységelem
- a dimenziótartó transzformációknak van inverze
- de nem kommutatív!
Affin transzformációk tulajdonságai
Az affin transzformációk megadhatóak egy lineáris transzformáció és egy eltolás segítségével, azaz ha affin transzformáció, akkor létezik és , hogy -ra:
A mátrix-vektor szorzást ilyen sorrendben végezzük el, azaz: a matrix a bal-, a vektor a jobboldalon áll.
A megadás homogén koordináták segítségével egyetlen mátrix-vektor szorzással is felírható:
Ugyanis ekkor
Az affin transzformációk a baricentrikus koordinátákat érvényben hagyják (a baricentrikus koordináták affin invariánsak)
Affin transzformációk megadása
-ben egy affin transzformációt egyértelműen meghatároz általános állású pont és annak képe
Azaz, például síkban ha adott három általános állású
pont és ezek képei, rendre
akkor -ket -kbe átvivő transzformációra
Projektív transzformációk megadása
-ben egy projektív transzformációt egyértelműen meghatároz általános állású pont és annak képe.
Tehát síkban 4: legyen és , ekkor megadható P-re:
Transzformációk osztályozása
Nevezetes affin transzformációk
Eltolás
Minden pontot egy adott vektorral eltolunk:
Általában -vel jelöljük
Mátrix alakhoz homogén koordináták kellenek, választással és akkor a következő -es mátrixszal adható meg:
Hiszen ha homogén koordinátáit hasznájuk az pontnak, akkor
Tulajdonságok
Az eltolások az affin transzformációk egy kommutatív részcsoportját alkotják.
A inverze
Forgatás
Forgatás síkban (a tengely körül) szöggel:
Mátrix alakban:
Hasonlóan kaphatjuk meg és síkokon is.
Forgatás mátrixok
tengely körül: tengely körül: tengely körül: ahol és
Tulajdonságok
Az azonos tengely körüli elforgatások az affin transzformációk egy kommutatív részcsoportját alkotják.
A térbeli forgatások felírhatók egyetlen mátrix segítségével. (lineáris transzformáció)
Az eltolás és forgatás sorrendje nem felcserélhető!
A forgatás inverze az eredeti forgatás nagyságával megegyező, de ellentétes irányú elforgatás:
Tetszőleges forgatás
Tetszőleges orientáció előállítható a három forgatás egymás utáni használatával.
Tetszőleges tengely körüli forgatás
Az eddigieket használva:
- toljuk el a forgástengelyt az origóba ()
- forgassuk be az egyik tengely körül a másik kettő síkjába (pl.: )
- ebben a síkban a két tengely közül az egyikkel forgassuk be a másik tengelybe (pl.: )
- végezzük el a forgatást (pl.: -szel, de ez az új \X{\prime\prime} tengely körül forgat!)
- alkalmazzuk az eddigi transzformációk inverzeit
Azaz például:
Tetszőleges tengely körüli forgatás megadható egy egységvektorral, ami
a forgatás tengelyét adja, és egy szöggel.
Ezt írja le a Rodrigues formula, aminek felhasználásával:
Yaw, pitch, roll
Egy objektum függőlege- (yaw), kereszt- (pitch) és hossztengelye (roll) menti elfordulásait egyszerre adjuk meg.
Repüléstanban és robotikában előszeretettel használt megadási mód.
Gyakorlatilag megegyezik azzal, mintha három "közönséges" tengely menti forgatást használnánk.
Csak akkor működik helyesen, ha az objektum tengelyei egybe esnek a koordináta-rendszer tengelyeivel.
Legtöbb API támogatja.
Mozgás-transzformációk
Az eltolások és tengely körüli elforgatások kombinációjaként leírható transzformációkat mozgás-transzformációknak nevezzük.
A tárgyak alakját és méretét nem változtatják.
Méretezés
Az tengelyek mentén "széthúzzuk", vagy "összenyomjuk" az alakzatot, azaz más léptéket választunk.
Mátrix alakban:
Speciális eset: tükrözés
Ha valamelyike negatív
- ha egy negatív: tükrözés az irányra merőleges síkra
- ha kettő negatív: tükrözés egy tengelyre
- ha mindhárom negatív: középpontos tükrözés
Ha páratlan számú negatív együttható van, akkor a sodrásirány is megváltozik!
Az bázisvektorokat felhasználva, ha lineáris transzformáció, akkor
ha egy transzformáció mátrixának determinánsa negatív, akkor a sodrásirány (a tárgyak térbeli irányítása) megváltozik.
Speciális eset: vetítés
Ha valamelyike nulla
- ha egy nulla: az irányra merőleges síkra vetítünk
- ha kettő nulla: egy tengelyre vetítünk
- ha mindhárom nulla: az origóba vetítünk mindent...
A determináns nulla nincs inverz!
Nyírás

Ha például minden pontban az értékeket -vel arányos mértékben módosítjuk:
Általánosan:
Áttérés új koordináta-rendszerre
Tegyük fel, hogy az ortonormált bázisvektorok helyett át akarunk térni az ortonolmárt bázisra (az új bázisvektorok koordinátáit ismerjük a régi bázisban)
Mik lesznek az eddig koordinátákkal azonosított pont koordinátái az új bázisban? Azaz milyen -re teljesül, hogy ?
Ortonormált mátrix inverze a mátrix transzponáltja, így az új koordinátákat adó mátrixunk a következő alakú:
Ha az új origó koordinátája , akkor
Áttekintés
Kommutativitás
A mátrix szorzás nem kommutatív, úgyhogy általaban nem igaz, hogy Ez jó, mivel általában a transzformációk sem kommutatívak.
Transzformációs mátrixok determinánsai
A méretezésnél láttuk, hogy ha egy vagy három együtthatója negatív a transzformációnak, akkor az megfordítja a sodrásirányt.
Általános esetre megfogalmazva:
- Ha , akkor a sodrásirány változatlan marad
- Ha , akkor a sodrásirány megfordul
Normálvektorok transzformációja
Legyen egy szakasz a síkban, normálvektorral. Legyen az tengely mentén kétszeres nyújtást leíró transzformáció.
Probléma: -t megkaphatjuk, ha eltranszformáljuk a két végpontját. Mi a helyzet normálvektorával? lesz? Nem!
Vizsgáljuk a normálvektor által megadott érintősík egyenletét!
Legyen az érintősík egy pontja, ekkor akkor és csak akkor van rajta a síkon, ha
Ekkor testzőleges (invertálható) transzformáció mellett:
A skaláris szorzat és a mátrix szorzás szabályai alapján kapjuk, hogy
Azaz a normálvektorokat az mátrix helyett annak inverztranszponáltjával kell szorozni!
Megjegyzés
A sík affin transzformációit egyértelműen meghatározza három független pont és azok képe.
A tér affin transzformációit egyértelműen meghatározza négy független pont és azok képe.
Projektív transzformáció
A színterünk képét akarjuk előállítani: vetíteni egy síkra
Az ember által látott képet nem lehet előállítani affin transzformációk segítségével. A "távolodó" párhuzamosok összetartanak, nem maradnak párhuzamosak.
Ez a látvány előállítható középpontos vetítéssel. Ez a transzformáció a homogén térben lineáris transzformáció.
Az affin transzformációk nem "bántották" az ideális elemeket, a fentiekhez azonban ez "kell".
Általános eset
Ha egy homogén transzformációs mátrix utolsó sora nem , akkor az olyan homogén lineáris transzformáció, ami az euklidészi térnek nem lineáris transzformációja.
Párhuzamos vetítés (ortogonális)
A mátrix ami megadja egyszerű, például síkra való vetítést:
Perspektív transzformáció
Középpontos vetítést valósít meg.
Az origóból a tengely mentén "nézünk" a térre.
A látótérnek egy csonkagúla felel meg.
A transzformáció a szem pozícióban találkozó vetítő egyenesekből párhuzamosakat csinál.
A csonkagúlát egy téglatestté transzformálja.
Paraméterei:
- a gúla függőleges nyílásszöge
- a gúla alapjának az oldalainak az aránya
- a közeli vágósík távolsága
- a távoli vágósík távolsága
Homogén osztás
Mivel egy "valódi" projektív transzformáció utolsó sora nem , ezért transzformáció után, általános esetben.
Ha ezt a pontot az eukleidészi térbe szeretnénk átvinni, akkor végig kell osztanunk -vel (ha ).
Középpontos vetítés
Az origó, mint vetítési középpont és egy, attól a tengely mentén egységre található, síkkal párhuzamos vetítősíkra való vetítés mátrixa: Homogén osztás után (-vel) a fentit kapjuk.
Megjegyzés
A sík projektív transzformációit egyértelműen meghatározza négy független pont és azok képe.
A tér projektív transzformációit egyértelműen meghatározza öt független pont és azok képe.
Transzformációs mátrixok - összefoglalás
Mi történik, ha a vektorunk negyedik koordinátája nulla (vagyis ha vektort azonosít a számegyenes)?
Az eltolás rész nem hat rá!
Figyeljünk: nem mindenhol szoroznak jobbról a vektorral!
Források
- Diasor
- Affine transformations in 5 minutes - youtube
- Affine transformation - wikipedia
- Affine transform interactive demo (2D)
- Perspective projection matrix (math for game developers) - youtube
Görbék, felületek és a fény útja
Egyszerű görbék és felületek
A görbéket, felületeket egy-egy ponthalmaznak tekintjük.
Hogyan adjuk meg ezeket a halmazokat?
- explicit:
- parametrikus:
- implicit:
Görbék
Görbék transzformációja
Hogyan transzformálhatunk görbéket a különböző megadási módokban?
- Explicit:
- Függőleges eltolás és nyújtás: függvényérték módosítása
- Vízszintes eltolás és nyújtás: a paraméter módosítása
- Függőleges eltolás és nyújtás: függvényérték módosítása
- Parametrikus: az eredménypont transzformációja
- Implicit: a paraméter transzformációja inverzzel
Parabola
Az tengelyű, fókuszpontú parabola egy
- Implicit egyenlete:
- Explicit egyenlete:
- Parametrikus egyenlete:
Mi van ha a pontba akarjuk eltolni az origóból a parabolát?
Az implicit és az explicit alakban be kell vinni a koordinátákat. (pl. implicitből lesz)
Parametrikus alakban egyszerűen lesz az új alak.
Kör
A középpontú, sugarú kör egy
- Implicit egyenlete:
- Explicit alakban nem tudjuk az egész kört leírni egy függvénnyel
(De két darabban menne, pl.: mellett , ahol ) - Parametrikus egyenlete: , ahol
Ellipsis
A középpontú, nagytengelyével az tengellyel párhuzamos, nagytengelyű és kistengelyű ellipszis egy
- Implicit egyenlete:
- Explicit alakban ugyan az a probléma, mint a körnél.
- Parametrikus egyenlete: , ahol
De mi van, ha nem akarjuk, hogy tengellyel párhuzamosak legyenek a tengelyeink?
- Implicit egyenlet: ez munkás(nak tűnik és habár nem az, de nekünk most nem kell...)
- Parametrikus egyenlete: bázisccsere! Ha az új tengelyek , akkor
, ahol
Szakasz
Legyen adott két pont, . A két ponton átmenő egyenes parametrikus egyenlete: ahol
Ha , akkor az pontokat összekötő egyenes szakaszt kapjuk.
Görbék parametrikus alakja
Derivártak:
Ha a görbét egy mozgó pont pályájának tekintjük, akkor az első derivált a sebességnek tekinthető, a második agyorsulásnak stb.
Görbe érintőegyenese
A görbe első deriváltja
Felületek
Felületek megadása:
- Explicit:
- Implicit:
- Parametrikus:
Matematikában általában a felfelé mutató tengelynek a tengelyt tekintik
Az alábbi képletek is ennek megfelelően adják a "várt" képet Grafikában viszont sokszor az mutat felfelé!
Felületek felületi normálisa
A felület érintősíkjának normálisa
Ha a parametrikus alakban adott a felület:
Implicit alakban adott felületnél , ahol
Gömb
Implicit egyenlet:
Parametrikus egyenlet:
Ellipszoid
Implicit egyenlet:
Parametrikus egyenlet:
Egyszerű paraboloid
Parametrikus egyenlet:
A fény útja
Jelölések
- a megvilágító, a fényt "adó" pont felé mutató vektor, ekkor a beesési irány .
- a felületi normális.
- egységvektorok.
- az és az által bezárt szög.
Ideális tükröződés
Visszaverődési törvény
A beesési irány (), a felületi normális (), és a kilépési irány () egy síkban van, valamint a beesési szög () megegyezik a visszaverődési szöggel ()
Visszaverődési irány
Általános esetben, egy beeső vektorból a visszaverődési- vagy tükörirány:
Mivel , és egységnyi hosszúak.
Ideális törés
Snellius-Descartes törvény
A beesési irány (), a felületi normális (), és a törési irány () egy síkban van, valamint , ahol az anyagok relatív törésmutatója.
Törési irány
Snellius-Descartes törvény:
Források
Raycasting
- Raycasting
- Az algoritmus
- Sugarak indítása
- Metszések
- Parametrikus sugár és implicit felület metszéspontja
- Parametrikus sugár és parametrikus felület metszéspontja
- Sugár és implicit sík metszéspontja
- Sugár és normálvektoros sík metszéspontja
- Sugár és parametrikus sík metszéspontja
- Sugár és háromszög metszéspontja I.
- Sugár és háromszög metszéspontja II.
- Sugár metszése poligonnal
- Sugár és gömb metszéspontja
- Sugár és transzformált objektumok metszése
- Sugér metszése AAB-vel
- Források
Tekintsünk minden pixelre úgy, mint egy kis ablakra a világra.
Milyen színértéket vegyen fel ez a pixel? Nézzük meg, mi látszik onnan a világból és az alapján rendeljünk hozzá a pixelhez egy színt!
Az algoritmus
for each pixel:
cast a ray into the scene
for each object in scene:
check if the ray intersects the object
set pixel to the color of the closest object
Sugár
A sugárnak van
- egy kiindulási pontja
- egy iránya
A parametrikus sugár: ahol (félegyenes).
?, ? sugár kezdőpontja, sugár mögötti részek.

Sugarak indítása
A szempozcióból indítunk sugarakat minden pixel középpontján keresztül
Most: középpontosan szeretnénk vetíteni egy kamerába, a vetítési sík egy négyszögletes részét megfeleltetve a képernyőnek.
Kamera tulajdonságok
- Szempozíció (eye),
- Egy pont amire néz (center),
- Felfele irányt megadó vektor a világban (up),
- Nyílásszög, amekkora szögtartományt lát (fov),
- Vetítővászon mérete. Most legyen adott:
Ezek segítségével fogjuk megadni pixel világbeli koordinátáit.

Keressük a kamera saját (jobbkezes) koordináta-rendszerét.
- Nézzen a kamera irányba!
- Az tengely legyen merőleges mind -re, mind az irányra!
- Az tengely merőleges -ra és -re is:
Pixel koordináták
Legyen az pixel középpontja, a vetítősík egységnyi távolságra a nézőponttól!
Ekkor:
Ahol

A sugár egyenlete
A sugár egy félegyenes, amit kezdőpontjával és irányvektorával adhatunk meg.
Legyen a sugár kezdőpontja, pedig az irányvektora, ekkor megadja a sugár összes pontját.
Most a sugarak kezdőpontját az előbbieknek megfelelően számolhatjuk, azaz
A sugár irányvektora pedig
Metszések
A sugárkövető programok futásidejük döntő részében metszéseket fognak végezni.
Nézzük meg néhány egyszerű geometriai elemmel vett metszetét a sugárnak.
A sugarak mindig a korábban is látott alakú, ahol feltesszük a továbbiakban, hogy .
Ekkor a sugárparaméter éppen a pont távolsága -tól.
Parametrikus sugár és implicit felület metszéspontja
Legyen adva egy implicit egyenlet, ami meghatározza a metszeni kívánt felületet. ()
A sugarunk egyenlete -re meghatározott egy pontot a térben helyettesítsük be ezt a képletet az implicit egyenletbe!
Tehát a következő egyenletet kell megadnunk -re:
A kapott -től függően a következő esetek állhatnank fenn:
- Ha , akkor a sugarunk előtt van a felület és metszi
- Ha , akkor a sugár kezdőpontja a felületen van
- Ha , akkor a sugár "mögött" van a felület és metszi a sugár egyenese a felületet (de nekünk kell!)
Parametrikus sugár és parametrikus felület metszéspontja
Legyen adva egy parametrikus felület.
Kell találni egy olyan sugárparamétert, amihez létezik , hogy
Ez három ismeretlenes (), három egyenletes ( koordinátáként egy) egyenletrendszer.
A ugyanúgy ellenőrizhető, mint előbb, de most az -re is figyeljünk, hogy a felületünk paramétertartományának megengedett részén van-e (általában kell)!
Sugár és implicit sík metszéspontja
Síkot megadhatunk implicit alakban:
A fenti sugár egyenese metszi a síkot, ha
Ezt -re átrendezve adódik
Látható a sík a nézőpontunkból, ha
Sugár és normálvektoros sík metszéspontja
Legyen a sík egy pontja, a normálvektora.
Legyen ez egyenes egy pontja, az irányvektora.
Az egyenes egyenlete:
A sík egyenlete: minden pontja a síknak kielégíti ezt az egyenletet.
Behelyettesítve -t a helyére:
ha
A sugár metszi a síkot, ha .
Ha , akkor az egyenes párhizamos a síkkal, és így vagy nincs metszéspontjuk, vagy az egyenes a síkon fut.
Sugár és parametrikus sík metszéspontja
Síkot megadhatunk egy pontjával és kifeszítő vektorokkal is:
Metszéspont a sugár egyenesével: keressük és -t úgy, hogy
Beírva a képletet adódik
Átrendezve kapjuk, hogy
Ez három ismeretlenes, három lineáris egyenletből álló egyenletrendszer, ami megoldható, ha lineárisan nem összefüggő.
Mátrix alakban:
Látjuk a síkot, ha (most a felület paramétertartománya, ez teljesülni fog)
Sugár és háromszög metszéspontja I.
A háromszög egyértelműen megadható három csúcsával.
Ha a háromszög csúcsai, akkor a hozzátartozó sík egy parametrikus megadésa
A korábbi jelölésekkel: és

Ez egyben egy baricentrikus megadása is, hiszen átrendezve kapjuk, hogy
ahol az együtthatók -re összegződnek.
Elvégezve tehát a parametrikus síkkal a metszést, megkapjuk a baricentriukus koordinátáit a sugár síkkal való metszéspontjának. A sugárparamétert ne felejtsük el ellenőrizni!
Utolsó lépésként ellenőriznünk kell, hogy a metszéspont a háromszögön belül van-e. Ez pontosan akkor teljesül, ha
Sugár és háromszög metszéspontja II.
A háromszög egyértelműen megadható három csúcsával.
Ha a háromszög csúcsai, akkor a hozzátartozó sík pont-normálvektoros implicit megadásához a sík
- egy pontja bármelyike
- normálvektora
ahol a vektorális szorzatot jelöli, és ekkor egységnyi hosszúságú.
Először számítsuk ki az egyenes és a háromszög síkjának metszéspontját, ez legyen (már ha létezik).
Legyenek a pont -re vonatkoztatott baricentrikus koordinátái, úgy hogy
akkor, és csak akkor van a háromszögön belül, ha
Pont a háromszögön vizsgálat
Tudjuk, hogy . Ekkor ill
A gyorsabb számolásértvegyük a fentiek egy síkra vett vetületét.
A koordinátasíkok közül (, vagy ) arra vegyük a háromszög 2D vetületét, amelyre a háromszög vetületének területe a legnagyobb! a héromszög és sík normálisa leginkább "egyálású".
A vetülethez egyszerűen elhagyjuk vagy egyenletét, megfelelően.
Azt a tengelyt kell választani, amelyik mentén a legnagyobb a háromszög normálvektorának abszolút értéke, így biztos nem fordulhat elő, hogy a háromszög merőleges a síkra, és csak egy szakasz marad belőle.
Pl. legyen a a választott tengely. Ekkor
Behelyettesítve -t, és rendezve:
Rendezve -re kapjuk:
A nevező csak degenerált háromszög esetén lehet nulla.
akkor, és csak akkor van a háromszögön belül, ha
Sugár metszése poligonnal
Tegyük fel, hogy a poligonunk csúcsai egy síkban vannak, ekkor a metszés két lépésben történik
- A sugarat metsszük el a poligon síkjával
- Döntsük el, hogy a metszőpont a poligonon belül van-e
A másodikat egy síkban érdemes csinálni (vagy a poligon síkjában, vagy a poligon valamely koordinátatengelyre vett vetületének síkjában)

Pont-poligon tartalmazás teszt síkban
A pont a poligonon belül van, ha tetszőleges irányú, belőle indított sugárnak páratlan számú metszéspontja van a poligon oldalaival. (azaz a sugarat a poligon összes oldalszakaszával el kell metszeni)
Konkáv és csillag alakú poligonra is működik.

Sugár metszése szakasszal
A poligon csúcspontjai közötti szakasz parametrikus alakja:
Ezt kell metszeni a alakú sugárral
Most: a pont az a pont, amiről el akarjuk dönteni, hogy a poligonon belül van-e, tetszőleges.
Legyen !
Így a egyenletet csak koordinátára kell megoldani.
Keressük meg, hogy hol metszi a oldal egyenese a sugarat ( melyik -re lesz ?)
Azaz
-t kifejezve:
Innen megkapjuk azt az koordinátát -be behelyettesítve, ahol a sugér metszi a szakaszt.
Ha : a sugár nem metszi a szakaszt (csak az egyenesét).
Ha : a sugár egybeesik a szakasszal, vagy mögötte van a metszéspont.
Sugár és gömb metszéspontja
Az sugarú, középpontú gömb implicit egyenlete:
Ugyanez skalárszorzattal felírva: ahol
Legyen az egyenes egy pontja, az irányvektora.
Ekkor az egyenes egyenlete:
Behelyettesítve a gömb egyenletébe ezt kapjuk:
Kifejtve:
Ez másodfokú egyenlet -re (minden más ismert).
Legyen
- Ha , két megoldás van, az egyenes metszi a gömböt.
- Ha , egy megoldás van, az egyenes érinti a gömböt.
- Ha , nincs valós megoldás, az egyenes nem metszi a gömböt.
Sugárparamétert ezután ellenőrizni kell ().
Másodfokú egyenlet megoldása
Elméletileg a megoldás megkapható esetben:
Gyakorlatilag baj van, ha
- Átalakítással megkapjuk, hogy formában felírható a két gyök (Citardauq Formula)
Gyakorlatilag akkor is baj van, ha
- Ekkor , vagyis előjelétől függően vagy vagy pedig elveszít az értékes tizedesjegyeket.
- Számítsuk ki az egyik gyököt azon az ágon, amelyiken nem vonunk ki egymásból két közrl azonos pozitív számot, a másik gyököt pedig a Viète-formulákból
- Azaz például ha , akkor és
Sugár és transzformált objektumok metszése
Legyen egy adott objektum transzformációs mátrixa.
Feladat: Keressük sugár és az -mel transzformált objektum metszéspontját!
Probléma: Hogyan transzformálunk egy gömböt? Pontonként? Képletet írjuk át?
Megoldás: transzformáljuk inkább a sugarat!
Tétel: Az sugér és az -mel transzformált objektum metszéspontja az -el transzformált sugár és az objektum metszéspontja.
- , homogén transzformáció
- Sugár kezdőpontja:
- Sugár iránya: . Így nem hat ré az eltolás.
- Transzformált sugár:
Metszetvizsgálat: használjuk -t!
Metszéspont: , akkor az eredeti térben
Távolságokaz újra kell számolni az eredeti térben!
Normálvektorok: helyett (inverz-transzponált)
Sugér metszése AAB-vel
AAB axis aligned box, olyan téglatest, aminek az oldallapjai a koordinátasíkjainkkal párhuzamosak.
Legyen a sugarunk alakú, ahol
a téglatestet pedig adjuk
meg átlójának két pontjával, és segítségével ()!
Tegyük fel, hogy a sugár kiindulópontja a doboztól balra helyezkedik el.

Legyen
Ha : merőleges az -tengelyre (pl. 2D-ben függőleges). Ekkor nincs metszéspont, ha , különben az -koordinátás számításokat kihagyhatjuk.
Ha , akkor legyen
Ha : cseréljük meg -t!
Ha :
Ha :
A fentit végezzük el az és koordinátákra is.
Ha : nem találtuk el a dobozt.
Ha : a doboz mögöttünk van.
Minden más esetben a sugarunk metszéspontjai a dobozzal és -ban lesznek (sorban a közelebbi és távolabbi metszéspontok)
Források
Fejlettebb raycasting
- Fejlettebb raycasting
Rekurzív sugárkövetés
Minden pixelre egymástól függetlenül határozzuk meg azok színét, oldjuk meg az árnylási és takarási feladatokat.

Fénykomponensek
A fény útját kétféle komponensre bontjuk:
- Koherens komponens:
- Az optikának megfelelő ideális visszaverődés és törés
- Továbbkövetjük a fény útját
- Inkoherens komponens:
- Minden egyéb
- Ezek közül mi csak az absztrakt fényforrás direkt megvilágítását vesszük figyelembe.
Jelölés
Két vektor skalár szorzatát az egyszerűség kedvéért most -vel fogjuk jelölni.
Az irányok jelölésére stb. betűket használjuk, de ezek továbbra is egységhosszú vektorok, azaz
Egyszerűsített illuminációs egyenlet

Sugárkövetés
Az felületi pontból az irányban kibocsátott radiancia
- A szempozícióból sugarakat indítunk minden pixelen keresztül
- A sugarak irányát -val jelöljük
- A sugár és a színtér objektumainak szemhez legközelebbi metszéspontja adja meg -et.
Emisszió
Ez a tag a felület saját sugárzását írja le az felületi pontból az irányába.
Ambiens fény
a felület, a környezet ambiens együtthatója. Az egyenlet ambiens tagja közelíti azt a fénymennyiséget, ami általánosan jelen van, minden felületet ér, azok helyzetétől és az absztrakt fényforrásoktól függetlenül. Célja a közelítések miatt elhagyott fénymennyiség pótlása.
Fényforrások
A figyelembe vett inkoherens visszaverődéseket foglalja össze a szummás tag.
Csak a fényforrások direkt hatását vesszük figyelembe, és csak akkor, ha az az felületi pontból látszik.
- a fényforrásból a felületi pontba mutató egységvektor.
- most csak a diffúz és spekuláris visszaverődést jellemző BRDF.
- a felületi normális és a fényforrás felé mutató vektor
által bezárt szög koszinusza egységnyi idő alatt -ből mennyi foton esik rá a felületre. - Ha az fényforrás teljesítménye felénk és pozíciója akkor
- láthatósági függvény: Mi van / van-e valami és a fényforrás között?
- , ha a fényforrás nem látható -ből
- , ha igen,
- , ha áttetsző objektumok vannak a kettő között.
- kiszámításához úgynevezett árnyéksugarakat indítunk -ből -felé, és az objektumokkal való metszését nézzük.
Négyzetes elhalás
Miért a metszéspont és a fényforrás távolságának négyzetével osztunk?
Tekintsünk egy pontszerű fényforrást, ami minden irányban egyenletesen sugároz radianciát.
Egyre távolodva tőle, a pontszerű fényforrás köré írt gömbön négyzetcentiméterenként mennyi fényt mérnénk? Radiancia osztva a távolsághoz tartozó gömb felületével, azaz
Tehát két különböző távolságban mért fénymennyiség aránya
Tükröződés
A tükörirányból érkező fényt arányban vesszük figyelembe.
az ideális tüköriránynak megfelelő beeső vektor.
Az az -ből induló, irányvektorú sugár legközelebbi metszéspontja színtérbeli elemmel.
kiszámítása azonos kiszámításával: rekurzió!
Új sugár: szempozíció helyett -ből indul, irány
Fénytörés
A törési-irányból érkező fényt arányban vesszük figyelembe.
a törésiránynak megfelelő beeső vektor.
Az az -ből induló, irányvektorú sugár legközelebbi metszőpontja színtérbeli elemmel.
kiszámítása megint azonos kiszámításával: rekurzió!
Új sugár: szempozíció helyett -ből indul, az iránya pedig
Színek
A képletek csak fénymennyiséggel számolnak, így valójában egyetlen hullámhosszon számítottuk ki a kamerába érkező fényt.
A hullámhossztól függ majdnem minden:
- A felület és a fényforrások által kibocsátott fény:
- A felület fényvisszaverő tulajdonsága (BDRF, közelítő és koherens együtthatók):
- ideális törésirány:
Tehát el kell végeznünk a számítást a látható fénytartomány minden hullámhosszára.
Ehelyett rendszerint csak néhány hullámhosszon.
Gyakorlatban sokszor csak RGB színhármasnak megfelelően.
Önárnyékolás
A numerikus pontatlanságok miatt előfordulhat, hogy a metszéspont valójában kissé a testen belül van.
Ilyenkor a fényforrások felé lőtt sugarak beleütközhetnek a kiindulási felületbe!
Vagy hagyjuk ki a metszésszámításokból a legutóbb metszett objektumot (ahonnan indulunk), vagy toljuk el a sugár kezdőpontját a felületi normális irányába.
Figyeljünk arra is, hogy mi is kell pontosan: a metszéspont helye vagy elég-e maga a metszés ténye?
Aliasing
Egyenközű pontonkénti mintavételezést csinálunk lényegében a mintavételezési frekvenciánál gyorsabb változások alias-olnak, azaz nem létező, alacsonyabb frekvenciás jelkomponensekként regisztráljuk őket.
Mintavételezés
Eddig csak pixelenként egyetlen sugarat indítottunk.
Ha többet indítunk, akkor a Nyquist-frekvencia nő.
Pixelenként egy szín kell csak a sugarak által behozott különböző színeket összegezni kell valahogy (pl. átlagolni)
De a több sugár eredményét is többféleképpen összegezhetjük (vagyis: szűrhetjük)
Egyenletes mintavételezéssel az alias nem szüntethető meg (csak ha a bejövő jel garantáltan nem tartalmaz túl magas frekvenciás komponenseket)
Azonban ha nem egyenletes a mintavételezés, hanem megfelelő eloszlás szerint történik, akkor az alias helyett véletlenszerő, nagyfrekvenciás zaj lesz a képen.
Ehhez a szemünk már alkalmazkodott!
Vegyük észre: a fényt fent végig részecskeként kezeltük.
Emiatt a fény hullám természetéből adódó jelenségeket (interferencia, diffrakció ) nem tusjuk visszaadni.
Mikor számítanak ezek?
- Az interferencia miatt látjuk olyan színben a páva tollait, vagy a szappanbuborék felszínét amilyenben látjuk.
- A diffrakció pedig a finom árnyjelenségek egy részében játszik szerepet.
Sugárkövetés gyorsítása
Metszésvizsgálat gyorsítása
Az algoritmus sebessége leginkább a metszésvizsgálat sebességétől függ.
Hogyan gyorsíthatnánk ezt?
Ne vizsgáljuk a metszést olyan objektumokra, amiket biztosan nem metsz a sugár!
Ne vizsgáljunk metszést olyan objektumokra, amik biztosan távolabbi metszéspontot adnak, mint a már megtalált!
Befoglaló keretek
Minden objektumot vegyünk körbe valamilyen kerettel amivel gyorsan lehet metszést számolni.
Ha egy sugár metszi az objektumot, akkor biztosan metszi a keretet is!
Fordítva is legyen minél nagyobb a valószínűsége! (Minél jobban közeltse a befoglaló test az igazit.)
Befoglaló gömb: másodfokú egyenlet megoldás.
Befoglaló doboz: élei a tengelyekkel párhuzamosak, Cohen-Sutherland szakaszvágó algoritmussal gyorsan számítható.

Konvex poliéderek
Egy -oldalú konvex poliéder felírható féltér metszeteként (féltér: )
Azaz az oldallapok síkjait kifelé mutató normálisokkal felírhatjuk alakban.
A korábban látott sugár-AAB metszés könnyen általánosítható erre az esetre!
Legyen a sugár
Legyen
Minden oldallapra:
Legyen a lap , egyenlete olyan, hogy az
lapnormális a poliéderből kifelé mutat.
- Számítsuk ki a sugár és az oldallap síkjának metszéspontját
- Ha , akkor
- Különben
Ha , akkor nincs metszéspont.
Különben a sugár egyenese -nél lép be és -nál hagyja el a konvex poliédert (azaz metszi a sugár a konvex poliédert, ha )
Hierarchikus befoglaló keretek
Kisebb kereteket nagyobb keretekbe fogjuk össze.
Fa struktúrát kapunk.
Egy részfát csak akkor kell kiértékelni, ha a gyökérrel van metszés.
Térfelosztó eljárások
Szabájos felosztás
Egy szabályos 3D ráccsal lefedjük az egészet színteret.
Előfeldolgozás: minden cellához feljegyezzük a beletartozó objektumokat.
Használat: csak azokkal az objektumokkal végzünk sugár metszést, amiknek a celláján a sugár áthalad.
Előnye: a vizsgálandó cellák gyorsan számíthatók szakaszrajzoló algoritmussal! (lsd.: raszterizáció)
Hátránya: feleslegesen sok cella, nagy részük üres teret fed le.

Oktális fá
Fa gyökere: a teljes színteret magában foglaló tengelyekkel párhuzamos élű befoglaló doboz (AABB)
Vágjuk ezt nyolc egyenlő részre!
Minden új dobozra: ha elég sok objektum van benne, akkor tovább osztjuk, különben megállunk.
Előny: az üres részeket nem osztjuk tovább feleslegesen.
Hátrány
- Bonyolultabb bejárás
- A fa mélysége elszállhat a gyakorlatban egy előírt mélység is adott, amit elérve már nem osztjuk tovább a cellákat.
Quadtree
Az oktális fa síkbeli változata
Az aktuális cellát mindig négy egyenlő részre osztjuk, a tengelyekkel párhuzamosan.
Kd fa
Probléma az oktális fával: mindig középen és mindig sík mentén vág, nem veszi figyelembe az objektumokat.
Oktális fa: keresési idő a fa magassága. De, az oktális fa kiegyensúlyozatlan.
kd-fa: minden lépésben egyetlen síkkal vágunk, ami egy tengelyre merőleges.
Sorrend:
Felező sík elhelyezése:
- térbeli középvonal módszer
- test középvonal módszer
- költség modell alapú módszer
Sugárkövetés hardverben
DXR
2018 óta NVIDIA GPU-kban hardveresen gyorsított raytracing érhető el.
Ez a DX 12 szabvány része lett.
Compute shaders fallback-kel kibővített támogatás van Pascal architektúráig lefelé.
De valódi hardveres raytracing csak Volta, Turing és Ampere és újabb architektúrákon van.
DXR 1.0
5 új shader típus:
- Raygeneration shader: sugarak előállítását végző shader
- Intersection shader: procedurális geometriákra; van beépített hardveres sugár-háromszög metszés, nem kell feltétlen megírni.
- Colsest hot shader: lényegében a fragment shader megfelelője; a legközelebbi metszéspontra egyszer lefutó shader.
- Anyhit shader: átlátszósági tesztek eldöntésére meghívódó shader bejárás közben; a meghívások sorrendjére nincs semmilyen garancia.
- Miss shader: ha nem volt metszett geometria, akkor ez hívódik meg. (Itt számíthatunk például égbolt színt, stb.)
DXR 1.1
Ami igazán érdekes, hogy innentől bármilyen shader-ben lehet hívni TraceRay parancsot (nem csak grafikus szerelőszalagbeliből, hanem compute shader-ből is!).
Illetve DispatchIndirect is van, ami rengeteg új lehetőséget ad.
Források
- Diasor
- BRDF - wikipédia
- Nyquist-Shannon sampling theorem - wikipedia
- Cohen-Sutherland algoritmus - wikipedia
- Bounding volume hierarchy - wikipedia
- Octree - wikipedia
- Quadtree - wikipedia
- k-d tree - wikipedia
Számítógépes grafika gyakorlat
Alapadatok
Idő: Hétfő, 8:00 - 10:00
Helyszín: Déli Tömb 2-219
Oktató: Horváth Anna Lili
Csoport: 1
Értékelés
- Órai munka
- Házi feladatok
- 2 kisbeadandó
- Nagybeadandó vagy évfolyam ZH
Források
1. Gyakorlat
- SDL ablakkezelés
- SDL rajzolás
- Double buffering
- Pontok generálása körön
Házi faladat
Nap sugarakkal - részletek a Teamsen
Források
2. Gyakorlat
SDL event kezelés és OpenGL inicializáció
Házi feladat
Kocka forgatással SDL-bre (még nem 3D-en). Részletek teams-en. Az egér pozícióját viszonyítjuk a középponthoz, 2 négyzetet tolunk el ellenkező irányban. A négyzetek sarkait egyenesekkel kötjük össze.
Források
3. Gyakorlat
Grafikus szerelőszallag, shaderek, uniformok;
Házi feladat
Mandelbrot-halmaz nagyítás, mozgatás-
Források
4. Gyakorlat
Vertex buffer és vertex array objektumok.
Házi feladat
Körvonal rahzolása vertexekkel.
Források
5. Gyakorlat
Transzformációk.
Házi feladat
Naprendszer
Források
6. Gyakorlat
Indices, parametric surfaces.
Házi feladat
Nagy tóruszon guruljanak kisebb tóruszok.
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
8. Gyakorlat
Textures
Házi feladat
Két mintavételező használata és mixelés
Források
9. Gyakorlat
Normals
Házi feladat
(TBA)
Források
Elmaradt óra
Ez az óra elmaradt, és nem tartottak pótló órát.
11. Gyakorlat
Skybox, OGLBase
Házi feladat
A Normals projektben található földgömböt készítsd el az OGLBase projekt eszközeivel. A programban legyen egy pontfényforrás, ami a földgömb körül kering. Ez legyen megjelenítve egy kis sárga hömb formájában.
Források
12. Gyakorlat
OGLBase, Transparency, Physics